below is the complete questions: part of the linear programming course:

1-

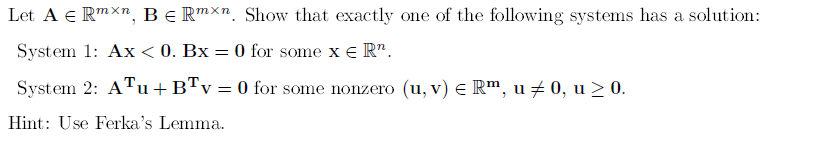
Let G = 1 1, 2 .... n't be a set containing the indicies of all the variables . Let Hi fori = 1 . ... m be mutually exclusive and collectively exhaustive subsets of G, defined as H}; C G. Hin HI; _ O for ` j = 1.... 10`` i f j, and Liz` HI, HE = G. Consider the following LP . REG 5. . . . D'ar SK Hi = ] . ... . M REH!` Ir ? O VPEG . where CERN, KER and bE I'M are parameters . Solve the above LP for the following scenarios :" ( a ) like 0 | 3T): 2 b} is nonempty and has extreme points? What is the maximal number and what is the minimal number of extreme points that such a set (an possess? (b) Let x1, . . . , xr represent all the extreme points of the following set: P1 = {x E Rn|Ax = b, x I_> D}? where A E Em)\" and b E R\Let A E MMX'n, BERMAN, Show that exactly one of the following systems has a solution :" System 1 : AX _ O. BOX _ O for Some YE |^! System ? : Au + BI'V = O for some nonzero ( U, V / { {M, 1 7 0, U ? O . Hint : Use Forka's LouimaLet A E TMXI GEMM and CERA. Let Q E ARM*i'm be an invertible matrix, and CE IM he the rector containing all ones . Consider the following L !' s " ICP - 1) & ICP - 21 1 : LP - 1 : \\CP - 2 : Illill . " Of x Tillll . " C X S. t . . AX = \\ S. t . . QAX P b * = 0 where p = Qle . Answer the following questions ! ( a ) Let &, " he the optimal objective function values corresponding to CP - 1 & CP - 2 respectively . Find the relationship between & and ] . ibj Let U. VE IM be the dual variables corresponding to LP - 1 & CP - ? respectively . Find the relationship between U and V