Below is the solved problem. I have to add the following constraint to this problem. Please show the formulas for each of the constraints.

Here is what I have so far... I don't necessarily know these are right.

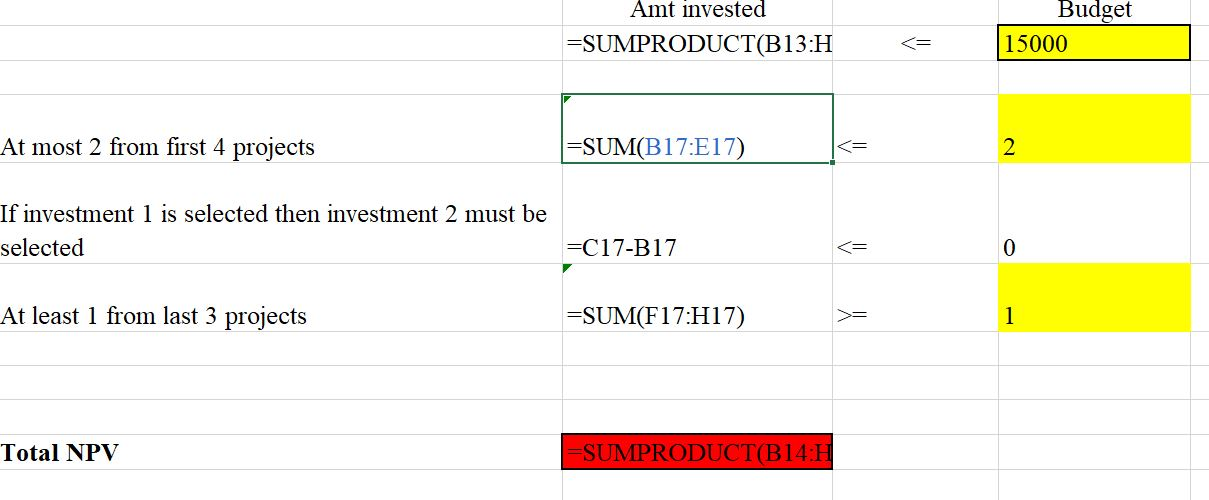
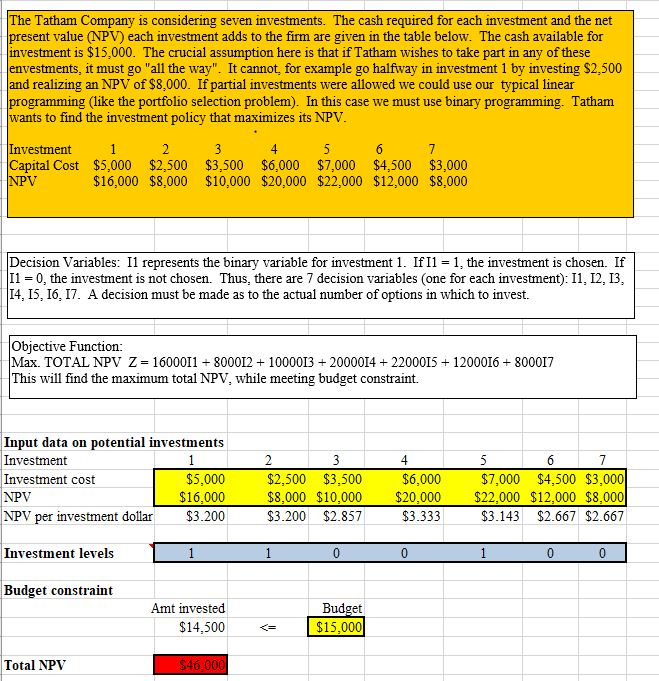
Below is the solution to the capital budgeting problem worked in class. Using the optimal solution that is given add the following constraints to the problem and solve it again. A. At most 2 of the first 4 projects can be selected. B. If investment 1 is selected, then investment 2 must also be selected. (However, this does NOT mean that if investment 2 is selected, then investment 1 must also be selected.) C. At least 1 of the last three projects (5-7) must be selected. D. Format your constraints appropriately. The Tatham Company is considering seven investments. The cash required for each investment and the net present value (NPV) each investment adds to the firm are given in the table below. The cash available for investment is $15,000. The crucial assumption here is that if Tatham wishes to take part in any of these envestments, it must go "all the way". It cannot, for example go halfway in investment 1 by investing $2,500 and realizing an NPV of $8,000. If partial investments were allowed we could use our typical linear programming like the portfolio selection problem). In this case we must use binary programming. Tatham wants to find the investment policy that maximizes its NPV. 3 Investment 1 2 4 5 6 7 Capital Cost $5,000 $2,500 $3,500 $6,000 $7,000 $4,500 $3,000 NPV $16,000 $8,000 $10,000 $20,000 $22,000 $12,000 $8,000 Decision Variables: 11 represents the binary variable for investment 1. If I1 = 1, the investment is chosen. If 11 = 0, the investment is not chosen. Thus, there are 7 decision variables (one for each investment): 11, 12, 13, 14, 15, 16, 17. A decision must be made as to the actual number of options in which to invest. Objective Function: Max. TOTAL NPV Z=1600011 + 800012 + 1000013 + 2000014 + 2200015 + 1200016 + 800017 This will find the maximum total NPV, while meeting budget constraint. 1 Input data on potential investments Investment Investment cost $5,000 NPV $16,000 NPV per investment dollar $3.200 2 $2,500 $3,500 $8,000 $10,000 $3.200 $2.857 4 $6,000 $20,000 $3.333 7 $7,000 $4,500 $3,000 $22,000 $12,000 $8,000 $3.143 $2.667 $2.667 Investment levels 1 0 0 0 0 Budget constraint Amt invested $14,500 Budget $15,000 Total NPV $46,000 Amt invested =SUMPRODUCT(B13:H Budget 15000