Below the problem is the starter code

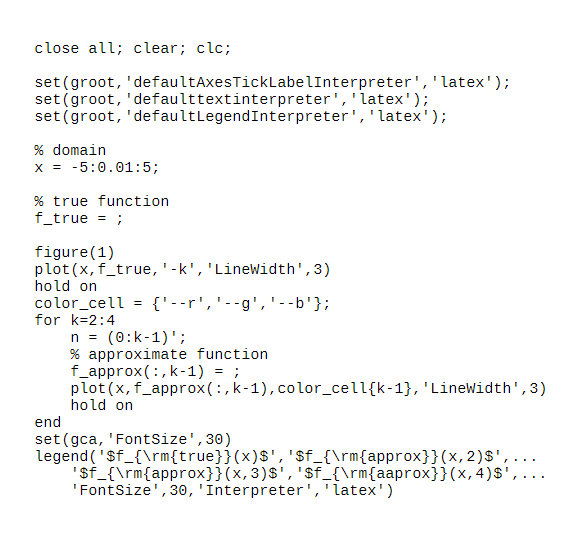
A function and its approximations (30 points) Consider n=0(3n)!x3n, that is, the power series obtained by keeping every third term in the Taylor expansion of exp(x). This power series corresponds to the true function ftrue(x)=31(exp(x)+2exp(x/2)cos(23x)). For any positive integer k, define the k term power series approximation fapprox(x,k):=n=0k1(3n)!x3n. Submit a MATLAB code (.m file) named YourlastnameYourfirstnameHW2p2.m that plots 2D line plots for the functions ftrue(x) (in black solid line) versus x[5,5] (in the horizontal axis). In the same figure window, plot fapprox(x,k) for k=2 (in red dashed line), k=3 (in green dashed line), k=4 (in blue dashed line). We shared a starter code YourlastnameYourf irstnameHW2p 2.m inside the CANVAS File section folder: HW Problems and Solutions. You only need to complete lines 11 and 20 in that starter code, then rename the file appropriately with your first and last names. Hint: Look up sqrt, exp, cos, sum, factorial, and power (.) in MATLAB documentation. Also, intuition suggests that as k increases, fapprox should get close to ftrue