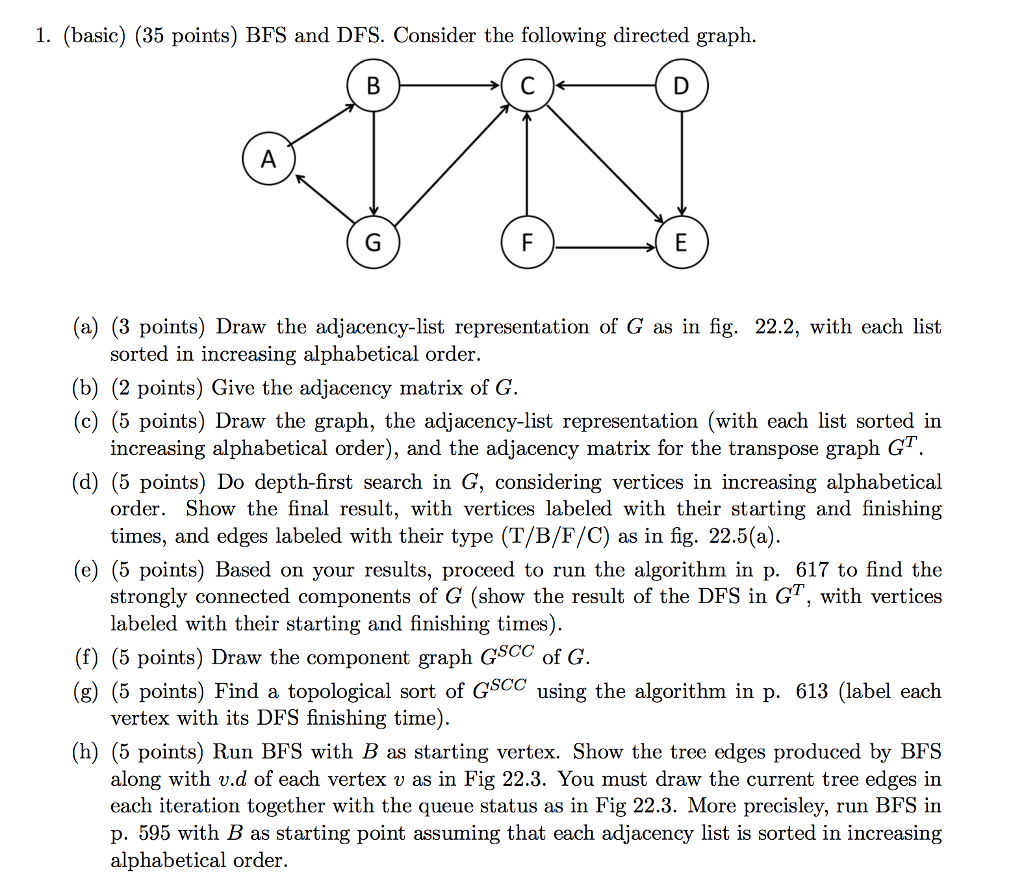
BFS and DFS. Consider the following directed graph. (a) Draw the adjacency-list representation of G as in fig. 22.2, with each list sorted in increasing alphabetical order (b) Give the adjacency matrix of G (c) Draw the graph, the adjacency-list representation (with each list sorted in increasing alphabetical order), and the adjacency matrix for the transpose graph G^T (d) Do depth-first search in G, considering vertices in increasing alphabetical order. Show the final result, with vertices labeled with their starting and finishing times, and edges labeled with their type (T/B/F/C) as in fig. 22.5 (a) (e) Based on your results, proceed to run the algorithm in p. 617 to find the strongly connected components of G (show the result of the DFS in G^T, with vertices labeled with their starting and finishing times). (f) Draw the component graph G^SCC of G (g) Find a topological sort of G^SCC using the algorithm in p. 613 (label each vertex with its DFS finishing time). (h) Run BFS with B as starting vertex. Show the tree edges produced by BFS along with v.d of each vertex v as in Fig 22.3. You must draw the current tree edges in each iteration together with the queue status as in Fig 22.3. More precisley, run BFS in p. 595 with B as starting point assuming that each adjacency list is sorted in increasing alphabetical order