Question: billions ) as a function of time t ( in years ) , with t = 0 corresponding to the beginning of 1 9 9
billions as a function of time in years with corresponding to the beginning of
a Find the function that expresses the world population in billions as a function of time in years
b If the world population continues to grow at the rate of approximately year, find the length of time in yr required for the world population to quadruple in size. Round your answer to two decimal places.
yr
c Using the time found in part a what would be the world population in billions of people if the growth rate were reduced to rRound your answer to two decimal places.
billion
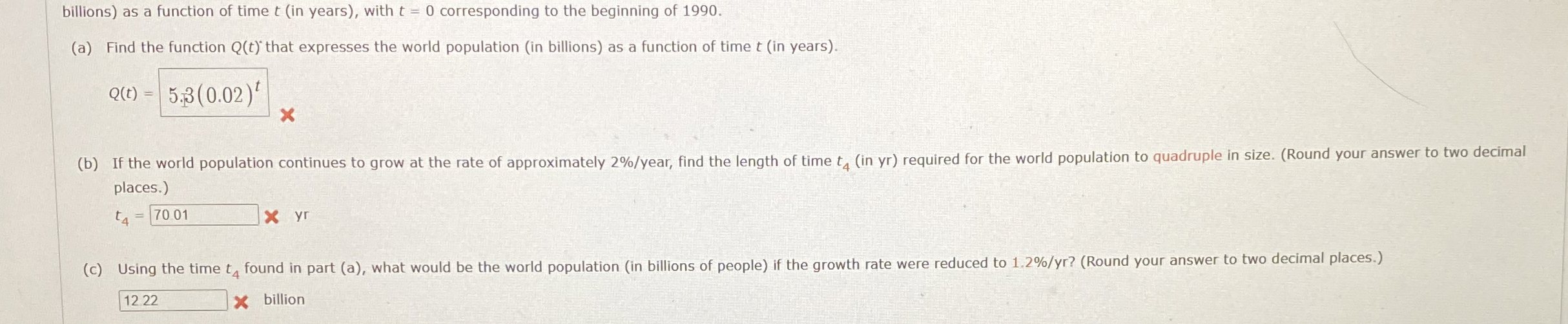
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


