Bisection
Newton
Ridder
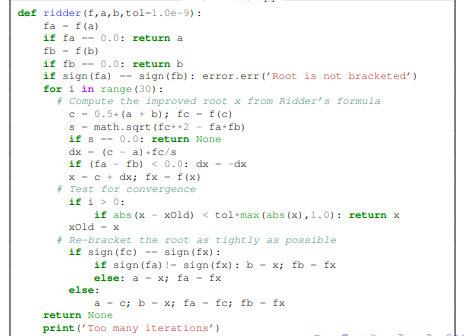
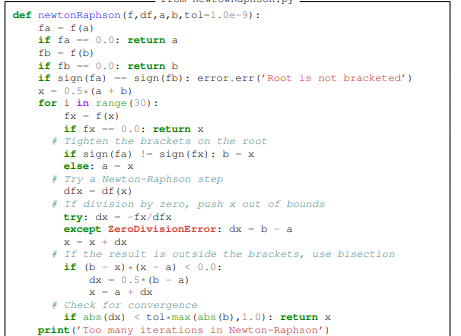
IN PYTHON PLEASE Implemeilt coding solutions to find the constant of proportionality k and the time of death td from the Background slides (background-pres.pdf, equations (1) slide 8, and equation (2) slide 9) using the following methods. (a) Bisection, (b) Newton's Method. (c Ridder's Method, Use a relative error convergence tolerance of 10-8 for both k and td. Output the initial parameters used in each call and the number of iterations, in addition to the final solution. In your readme.txt file, mention how you decided on the initial parameter for each function. Example python implementations of each method is in the slides for the chapter. Feel free to base your code on those examples. You should implement the plain Newton's method, not the safe version of the end of the slides. 1 72 +1 - + k 1 18+ k *) e* = 85 (1) 1 72 + td 1 + k 18+ ktd 98.6 (2) k IN PYTHON PLEASE from bisection.py def bisection(f,x1, x2, switch-1, tol-1.0e-9): fl - f(x1) if f1 -- 0.0: return x1 f2 - f (x2) if f2 -- 0.0: return x2 if sign(f1) -- sign(f2): error.err('Root is not bracketed') n - int (math.ceil(math.log(abs (x2 - xl)/tol) /math.log(2.0))) for i in range(n): x3 - 0.5+ (x1 + x2); f3 - f(x3) if (switch -- 1) and (abs (f3) > abs(f1)) and (abs (3) > abs (f2)): return None if f3 -- 0.0: return x3 if sign(f2)!- sign (f3): x1 - x3; fl - f3 else: x2 - x3; f2 - f3 return (x1 + x2)/2.0 def newtonRaphson (f, df, a, b, tol-1.0e-9): fa - f(a) if fa -- 0.0: return a fb - f(b) if fb -- 0.0: return b if sign (fa) -- sign (fb): error.err('Root is not bracketed') X - 0.5. (a + b) for i in range (30): fx - f(x) if fx -- 0.0: return x # Tighten the brackets on the root if sign (fa) !- sign (fx): b - x else: a - X + Try a Newton-Raphson step dfx - df (x) # If division by zero, push x out of bounds try: dx - fx/dfx except ZeroDivisionError: dx - b - a x - x + dx # If the result is outside the brackets, use bisection if (b - x) + (x - a) 0: if abs(x - xold) abs(f1)) and (abs (3) > abs (f2)): return None if f3 -- 0.0: return x3 if sign(f2)!- sign (f3): x1 - x3; fl - f3 else: x2 - x3; f2 - f3 return (x1 + x2)/2.0 def newtonRaphson (f, df, a, b, tol-1.0e-9): fa - f(a) if fa -- 0.0: return a fb - f(b) if fb -- 0.0: return b if sign (fa) -- sign (fb): error.err('Root is not bracketed') X - 0.5. (a + b) for i in range (30): fx - f(x) if fx -- 0.0: return x # Tighten the brackets on the root if sign (fa) !- sign (fx): b - x else: a - X + Try a Newton-Raphson step dfx - df (x) # If division by zero, push x out of bounds try: dx - fx/dfx except ZeroDivisionError: dx - b - a x - x + dx # If the result is outside the brackets, use bisection if (b - x) + (x - a) 0: if abs(x - xold)
