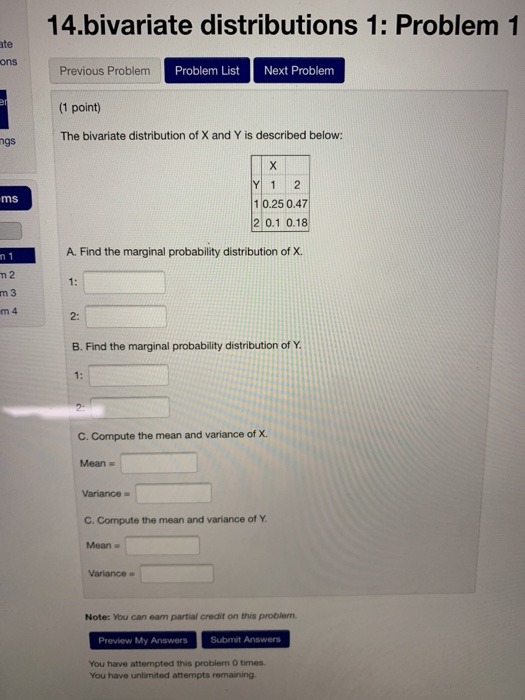
Question: Bivariate distribution Question 2 |3 Mark|: Consider the following system of linear equations: 3.333(1t. + 15920x3 + [0.333; = T953. 2.222(1r. + 16.1104} + 9.6[203'3
Bivariate distribution
Question 2 |3 Mark|: Consider the following system of linear equations: 3.333(1t. + 15920x3 + [0.333; = T953. 2.222(1r. + 16.1104} + 9.6[203'3 = 0.965. -l.561|.t. + 5.l792.r2 - [.6355x3 = 2.7M. with actual solution: [1, 0.5, -1]. it. Use Gaussian elimination and three-digit rounding arithmetic to solve the above linear gm compare the approximations to the actual solution. b. Repeat the exercise using Gaussian elimination with partial pivoting. c. Repeat the exercise using Gaussian elimination with sealed pivoting. (17) 1. Consider a random experiment that consists of throwing a dart at a triangle-shaped target with vertices at the (x, y) positions (-1, -1), (2, -1), and (-1, 2), resulting in outcome (x, y), the point where the dart hits. Assume that the dart always hits the target and that the probability distribution is uniform over the surface of the target. That is, the bivariate probability density function (pdf), fxY(x, y), has constant value C over the triangle and value 0 outside the triangle. Let the corresponding bivariate cumulative distribution function (CDF) be Fxv(x, y). a. Sketch a bird's-eye view, looking straight down from above, showing the borders and "footprint" of pdf fxY(x, y) on the x-y plane. b. Find the numeric value of pdf fxY(x, y) for x = 0, y = 0. Explain your work. c. Find the numeric value of CDF Fxy(x, y) for x = 0, y = 0. Explain your work.1. (25 pts/5pts each part) The figure shows a spherical shell with uniform volume charge density o = 1.76 nC/m', inner radius a = 15.0 cm, and outer radius b = 2.20a. What is the magnitude of the electric field (in N/C) at the following radial distances? (a) r = a/2.00 Qenc = 0 , so E = 0 (b) r = a Qenc = 0 , so E = 0 (c) r = 1.50a Only some of the total charge of the shell is contained in the Gaussian surface. Qenc = 0*Vsphere =[1.76 *101-9 C/m'] *4/3*pi*[(1.5a^3) - a^3] Area of Gaussian Surface = 4*pi* (1.5a)^2 E = Qenc/(Area of Gaussian Surface x Free Space Permittivity] = 10.5 N/c (d) r=b All of the total charge of the shell is contained in the Gaussian surface. Qenc = 0*Vsphere =[1.76 *101-9 C/m'] *4/3*pi*[(b^3) - a^3] Area of Gaussian Surface = 4*pi* (b)^2 E = Qenc/(Area of Gaussian Surface x Free Space Permittivity] = 19.8 N/c (e) r= 3.00b14.bivariate distributions 1: Problem 1 ite ons Previous Problem Problem List Next Problem (1 point) igs The bivariate distribution of X and Y is described below: X Y 1 2 ms 1 0.25 0.47 2 0.1 0.18 1 1 A. Find the marginal probability distribution of X. n 2 n 3 m 4 2 B. Find the marginal probability distribution of Y. C. Compute the mean and variance of X. Mean = Variance - C. Compute the mean and variance of Y. Mean = Variance . Note: You can earn partial credit on this problem. Proview My Answers Submit Answers You have attempted this problem 0 times You have unlimited attempts remaining