Bivariate normal distribution. The continuous random vector (X, Y) is said to have a normal distribution of parameters ?(1?,?12?,2?,?22?,?)? , where ?1?? and ?2?? are any real numbers,

??12?>0,?22?>0? and ??1?1,? if its density function is

?f(x,y)=2??1??2?(1??2)?1?exp(?2(1??2)1?[?12?(x??1?)2???1??2?2??(x??1?)(y??2?)+?22?(y??2?)2?])?

In the case of ?1?=2?=0? and ??12?=?22?=1,? the standard bivariate normal distribution is obtained and the expression of the density function acquires the simple expression that appears below, and whose graph appears in the Figure, when ??=0.?

?f(x,y)=2?(1??2)?1?exp(?2(1??2)1?(x2?2?xy+y2))?

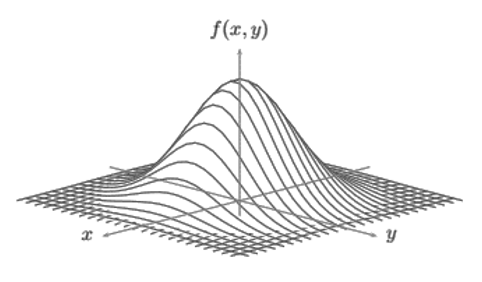
\f