BME $441/501$ Shape Interpolation Using Fourier Descriptors

Project

Fall $2023$

is

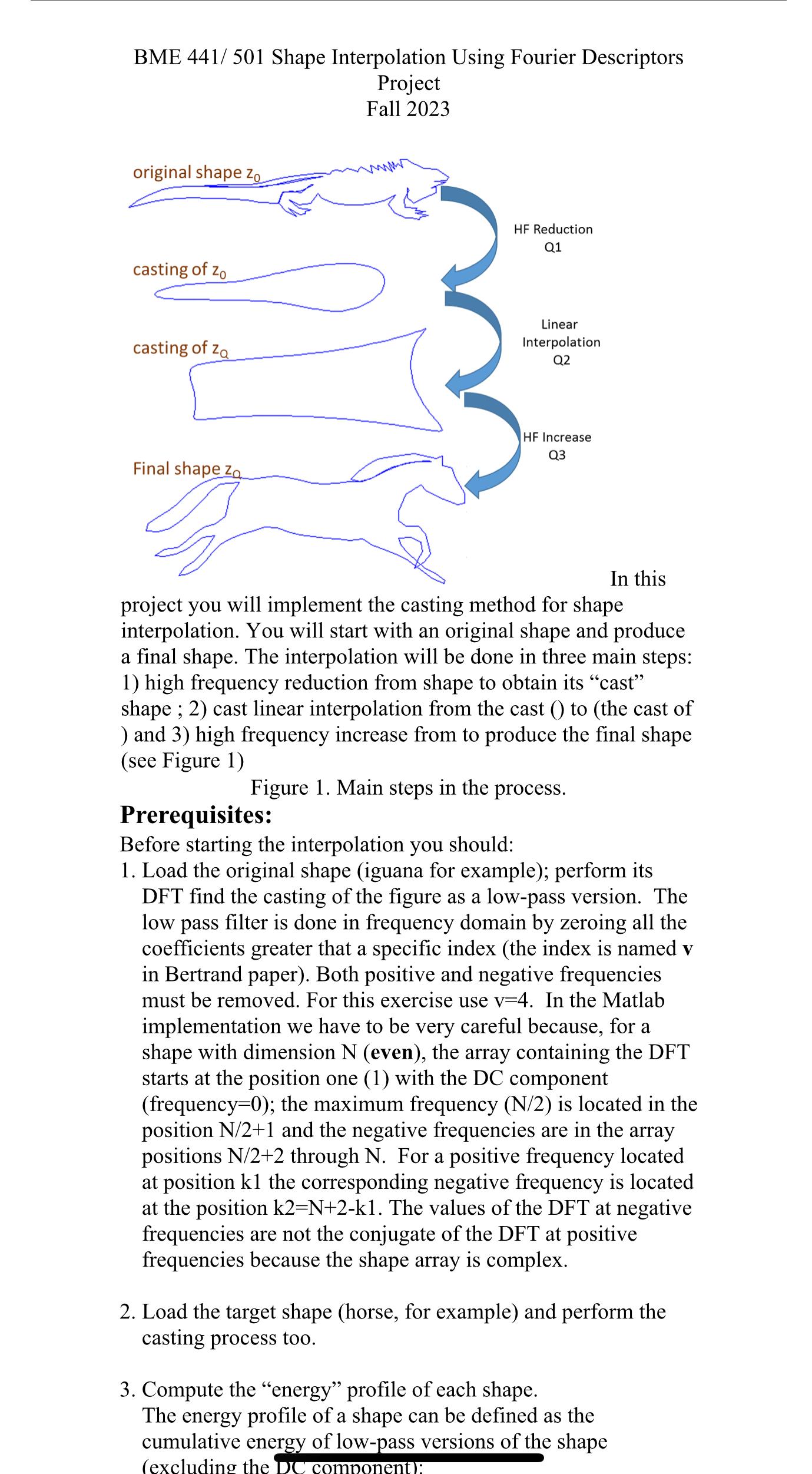
project you will implement the casting method for shape interpolation. You will start with an original shape and produce a final shape. The interpolation will be done in three main steps: $1)$ high frequency reduction from shape to obtain its "cast" shape ; $2)$ cast linear interpolation from the cast $()$ to $($the cast of $)$ and $3)$ high frequency increase from to produce the final shape $($see Figure $1)$

Figure $1.$ Main steps in the process.

Prerequisites:

Before starting the interpolation you should:

Load the original shape $($iguana for example$)$; perform its DFT find the casting of the figure as a low$-$pass version. The low pass filter is done in frequency domain by zeroing all the coefficients greater that a specific index $($the index is named $v$ in Bertrand paper$).$ Both positive and negative frequencies must be removed. For this exercise use $v=4.$ In the Matlab implementation we have to be very careful because, for a shape with dimension $N($even$),$ the array containing the DFT starts at the position one $(1)$ with the DC component $($frequency $=0$; the maximum frequency $(\frac{N}{2})$ is located in the position $\frac{N}{2}+1$ and the negative frequencies are in the array positions $\frac{N}{2}+2$ through N$.$ For a positive frequency located at position $k1$ the corresponding negative frequency is located at the position $k2=N+2-k1.$ The values of the DFT at negative frequencies are not the conjugate of the DFT at positive frequencies because the shape array is complex.

Load the target shape $($horse$,$ for example$)$ and perform the casting process too.

Compute the "energy" profile of each shape. The energy profile of a shape can be defined as the cumulative energy of low$-$pass versions of the shape