Both implementations of __contains__ have a worst case running time of 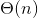, where n is the length of the list. You should get an EXACT expression for the running time each heuristic, and then convert that to a Theta bound.

4. Let n, m ezt. Let Ist be the list of numbers 0, 1, 2, ..., n-1. Deseribe a sequence of m-search operations on lst such that the total running time of the search operations using Heuristic +(move to front) is asymptotically greater than the total running time of the search operations using Heuristie 2 (swap). (Updated Jan 25) Describe a sequence of m search operations on Ist such that the total running time of the search operations using Heuristic 1 (move to front) is greater than the total running time of the search operations using Heuristic 2 (swap), subject to: i. If T is the running time for Heuristic 1 and T2 is the running time for Heuristic 2, then T1 T2 & 0(1) (i.e., the difference in running times is not bounded above by a constant). ii. In your running time analysis, only count the number of distinct nodes traversed by __contains_ per operation, and ignore other constant-time operations.3 By distinct we mean that the same node should only be counted once per search call, but is counted multiple times if it is traversed in multiple search calls. You may (but are not required to) assume that m is greater than some function of n (e.g., "Assume m >n" or Assume m > n2") in your analysis, as long as this is clearly stated. Your solution to this question should begin with a clear description of the search operations, followed by analyses for the total running time for both heuristics. These analyses should have the same format as Question 2, (new) except they should only count the number of nodes traversed, as described above. Heuristic 1 (move to front): move the item being searched for to the front of the list. (Do nothing if the item is already at the front of the list.) For example, if we search for 40 in the following list: first 10 20 30 40 50 60 None The list is mutated to become: first 40 10 20 30 50 60 None Heuristic 2 (swap): swap the item being searched for with the item immediately before it. (Do nothing if the item is already at the front of the list.) For example, if we search for 40 in the following list: first 10 20 30 40 50 60 None The list is mutated to become: first 10 20 40 30 50 60 None 4. Let n, m ezt. Let Ist be the list of numbers 0, 1, 2, ..., n-1. Deseribe a sequence of m-search operations on lst such that the total running time of the search operations using Heuristic +(move to front) is asymptotically greater than the total running time of the search operations using Heuristie 2 (swap). (Updated Jan 25) Describe a sequence of m search operations on Ist such that the total running time of the search operations using Heuristic 1 (move to front) is greater than the total running time of the search operations using Heuristic 2 (swap), subject to: i. If T is the running time for Heuristic 1 and T2 is the running time for Heuristic 2, then T1 T2 & 0(1) (i.e., the difference in running times is not bounded above by a constant). ii. In your running time analysis, only count the number of distinct nodes traversed by __contains_ per operation, and ignore other constant-time operations.3 By distinct we mean that the same node should only be counted once per search call, but is counted multiple times if it is traversed in multiple search calls. You may (but are not required to) assume that m is greater than some function of n (e.g., "Assume m >n" or Assume m > n2") in your analysis, as long as this is clearly stated. Your solution to this question should begin with a clear description of the search operations, followed by analyses for the total running time for both heuristics. These analyses should have the same format as Question 2, (new) except they should only count the number of nodes traversed, as described above. Heuristic 1 (move to front): move the item being searched for to the front of the list. (Do nothing if the item is already at the front of the list.) For example, if we search for 40 in the following list: first 10 20 30 40 50 60 None The list is mutated to become: first 40 10 20 30 50 60 None Heuristic 2 (swap): swap the item being searched for with the item immediately before it. (Do nothing if the item is already at the front of the list.) For example, if we search for 40 in the following list: first 10 20 30 40 50 60 None The list is mutated to become: first 10 20 40 30 50 60 None