BST.Java

public class BST> implements Tree { protected TreeNode root; protected int size = 0; /** Create a default binary tree */ public BST() { } /** Create a binary tree from an array of objects */ public BST(E[] objects) { for (int i = 0; i current = root; // Start from the root while (current != null) { if (e.compareTo(current.element) 0) { current = current.right; } else return true; // e is found } return false; } @Override /** Insert element o into the binary tree * Return true if the element is inserted successfully */ public boolean insert(E e) { if (root == null) root = createNewNode(e); // Create a new root //root = new TreeNode(e); // Question: Why not do it this way? Itwould work. else { // Locate the parent node TreeNode parent = null; TreeNode current = root; while (current != null) if (e.compareTo(current.element) 0) { parent = current; current = current.right; } else return false; // Duplicate node not inserted // Create the new node and attach it to the parent node if (e.compareTo(parent.element) (e);

else parent.right = createNewNode(e); } size++; return true; // Element inserted successfully } protected TreeNode createNewNode(E e) { return new TreeNode(e); } @Override /** Inorder traversal from the root */ public void inorder() { inorder(root); } /** Inorder traversal from a subtree */ protected void inorder(TreeNode root) { if (root == null) return; inorder(root.left); System.out.print(root.element + " "); inorder(root.right); } @Override /** Postorder traversal from the root */ public void postorder() { postorder(root); } /** Postorder traversal from a subtree */ protected void postorder(TreeNode root) { if (root == null) return; postorder(root.left); postorder(root.right); System.out.print(root.element + " "); } @Override /** Preorder traversal from the root */ public void preorder() { preorder(root); } /** Preorder traversal from a subtree */ protected void preorder(TreeNode root) { if (root == null) return; System.out.print(root.element + " "); preorder(root.left); preorder(root.right); } /** This inner class is static, because it does not access any instance members defined in its outer class */ public static class TreeNode { protected E element; protected TreeNode left; protected TreeNode right; public TreeNode(E e) {

element = e; } } @Override /** Get the number of nodes in the tree */ public int getSize() { return size; } /** Returns the root of the tree */ public TreeNode getRoot() { return root; } /** Returns a path from the root leading to the specified element */ public java.util.ArrayList> path(E e) { java.util.ArrayList> list = new java.util.ArrayList(); TreeNode current = root; // Start from the root while (current != null) { list.add(current); // Add the node to the list if (e.compareTo(current.element) 0) { current = current.right; } else break; } return list; // Return an array list of nodes } @Override /** Delete an element from the binary tree. * Return true if the element is deleted successfully * Return false if the element is not in the tree */ public boolean delete(E e) { // Locate the node to be deleted and also locate its parent node TreeNode parent = null; TreeNode current = root; while (current != null) { if (e.compareTo(current.element) 0) { parent = current; current = current.right; } else break; // Element is in the tree pointed at by current } if (current == null) return false; // Element is not in the tree // Case 1: current has no left child

if (current.left == null) { // Connect the parent with the right child of the current node if (parent == null) { root = current.right; } else { if (e.compareTo(parent.element) parentOfRightMost = current; TreeNode rightMost = current.left; while (rightMost.right != null) { parentOfRightMost = rightMost; rightMost = rightMost.right; // Keep going to the right } // Replace the element in current by the element in rightMost current.element = rightMost.element; // Eliminate rightmost node if (parentOfRightMost.right == rightMost) parentOfRightMost.right = rightMost.left; else // Special case: parentOfRightMost == current parentOfRightMost.left = rightMost.left; } size--; return true; // Element deleted successfully } @Override /** Obtain an iterator. Use inorder. */ public java.util.Iterator iterator() { return new InorderIterator(); } public java.util.Iterator iterator(int index) { return new InorderIterator(index); } // Inner class InorderIterator private class InorderIterator implements java.util.Iterator { // Store the elements in a list private java.util.ArrayList list = new java.util.ArrayList(); private int current = 0; // Index of next element in the iteration public InorderIterator() { inorder(); // Traverse binary tree and store elements in list }

public InorderIterator(int index) { if (index size()) throw new IndexOutOfBoundsException(); inorder(); current = index; } /** Inorder traversal from the root*/ private void inorder() { inorder(root); } /** Inorder traversal from a subtree */ private void inorder(TreeNode root) { if (root == null) return; inorder(root.left); list.add(root.element); inorder(root.right); } @Override /** More elements for traversing? */ public boolean hasNext() { return current

BST Animation

import javafx.application.Application;import javafx.geometry.Pos;import javafx.stage.Stage;import javafx.scene.Scene;import javafx.scene.control.Button;import javafx.scene.control.Label;import javafx.scene.control.TextField;import javafx.scene.layout.BorderPane;import javafx.scene.layout.HBox;public class BSTAnimation extends Application { @Override // Override the start method in the Application class public void start(Stage primaryStage) { BST tree = new BST(); // Create a tree BorderPane pane = new BorderPane(); BTView view = new BTView(tree); // Create a View pane.setCenter(view); TextField tfKey = new TextField(); tfKey.setPrefColumnCount(3); tfKey.setAlignment(Pos.BASELINE_RIGHT); Button btInsert = new Button("Insert"); Button btDelete = new Button("Delete"); HBox hBox = new HBox(5); hBox.getChildren().addAll(new Label("Enter a key: "), tfKey, btInsert, btDelete); hBox.setAlignment(Pos.CENTER); pane.setBottom(hBox); btInsert.setOnAction(e -> { int key = Integer.parseInt(tfKey.getText()); if (tree.search(key)) { // key is in the tree already view.displayTree(); // Clears the old status message view.setStatus(key + " is already in the tree"); } else { tree.insert(key); // Insert a new key view.displayTree(); view.setStatus(key + " is inserted in the tree"); } }); btDelete.setOnAction(e -> { int key = Integer.parseInt(tfKey.getText()); if (!tree.search(key)) { // key is not in the tree view.displayTree(); // Clears the old status message view.setStatus(key + " is not in the tree"); } else { tree.delete(key); // Delete a key view.displayTree(); view.setStatus(key + " is deleted from the tree"); } }); // Create a scene and place the pane in the stage Scene scene = new Scene(pane, 450, 250); primaryStage.setTitle("BSTAnimation"); // Set the stage title

primaryStage.setScene(scene); // Place the scene in the stage primaryStage.show(); // Display the stage } /** * The main method is only needed for the IDE with limited * JavaFX support. Not needed for running from the command line. */ public static void main(String[] args) { launch(args); }}

BSTView.java

import javafx.scene.layout.Pane;import javafx.scene.paint.Color;import javafx.scene.shape.Circle;import javafx.scene.shape.Line;import javafx.scene.text.Text;public class BTView extends Pane { private BST tree = new BST(); private double radius = 15; // Tree node radius private double vGap = 50; // Gap between successive levels in the tree BTView(BST tree) { this.tree = tree; setStatus("Tree is empty"); } public void setStatus(String msg) { this.getChildren().add(new Text(20, 20, msg)); } public void displayTree() { this.getChildren().clear(); // Clear the pane if (tree.getRoot() != null) { // Display tree recursively displayTree(tree.getRoot(), getWidth() / 2, vGap, getWidth() / 4); } } /** Display a subtree rooted at position (x, y) */ private void displayTree(BST.TreeNode root, double x, double y, double hGap) { if (root.left != null) { // Draw a line to the left node getChildren().add(new Line(x - hGap, y + vGap, x, y)); // Draw the left subtree recursively displayTree(root.left, x - hGap, y + vGap, hGap / 2); } if (root.right != null) { // Draw a line to the right node getChildren().add(new Line(x + hGap, y + vGap, x, y)); // Draw the right subtree recursively displayTree(root.right, x + hGap, y + vGap, hGap / 2); } // Display a node Circle circle = new Circle(x, y, radius); circle.setFill(Color.WHITE); circle.setStroke(Color.BLACK); this.getChildren().addAll(circle, new Text(x - 4, y + 4, root.element.toString())); }}

Tree.java

import java.util.Collection;public interface Tree extends java.util.Collection { /** Return true if the element is in the tree */ public boolean search(E e); /** Insert element o into the binary tree * Return true if the element is inserted successfully */ public boolean insert(E e); /** Delete the specified element from the tree * Return true if the element is deleted successfully */ public boolean delete(E e); /** Get the number of nodes in the tree */ public int getSize(); /** Inorder traversal from the root*/ public default void inorder() { //throw new UnsupportedOperationException(); } /** Postorder traversal from the root */ public default void postorder() { } /** Preorder traversal from the root */ public default void preorder() { } @Override /** Return true if the tree is empty */ public default boolean isEmpty() { return size() == 0; }; @Override public default boolean contains(Object e) { return search((E)e); } @Override public default boolean add(E e) { return insert(e); } @Override public default boolean remove(Object e) { return delete((E)e); } @Override public default int size() { return getSize(); } @Override public default boolean containsAll(Collection> c) { // Left as an exercise return false;

} @Override public default boolean addAll(Collection extends E> c) { // Left as an exercise return false; } @Override public default boolean removeAll(Collection> c) { // Left as an exercise return false; } @Override public default boolean retainAll(Collection> c) { // Left as an exercise return false; } @Override public default Object[] toArray() { // Left as an exercise return null; } @Override public default T[] toArray(T[] array) { // Left as an exercise return null; }}

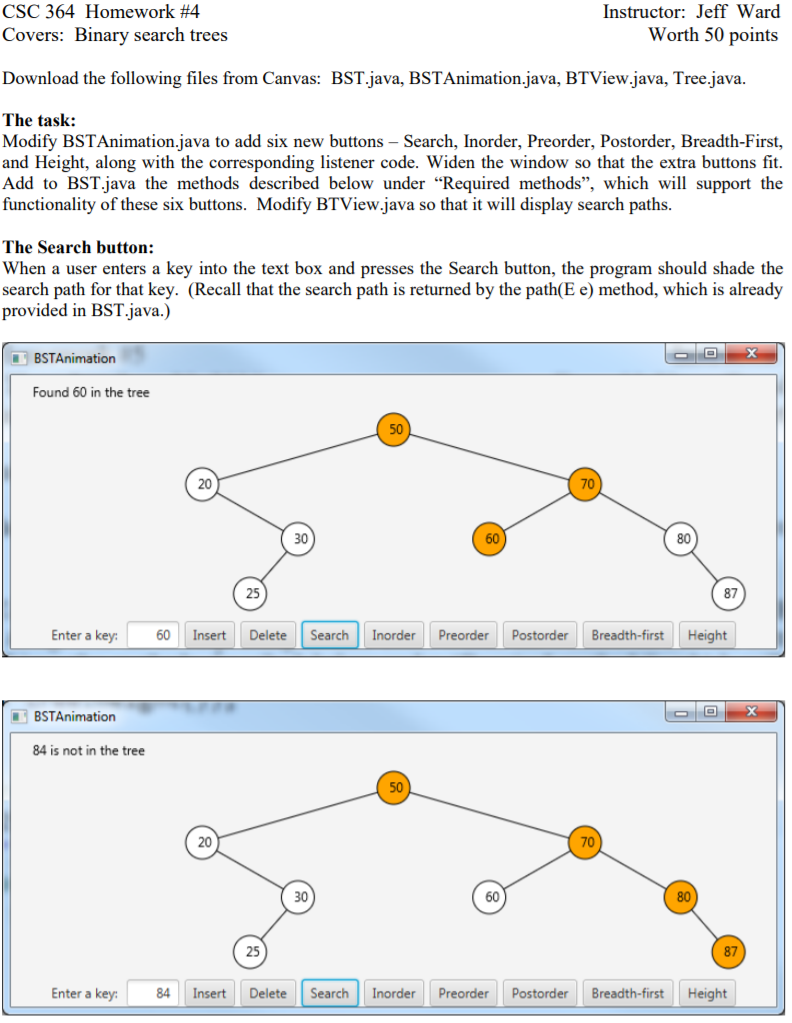
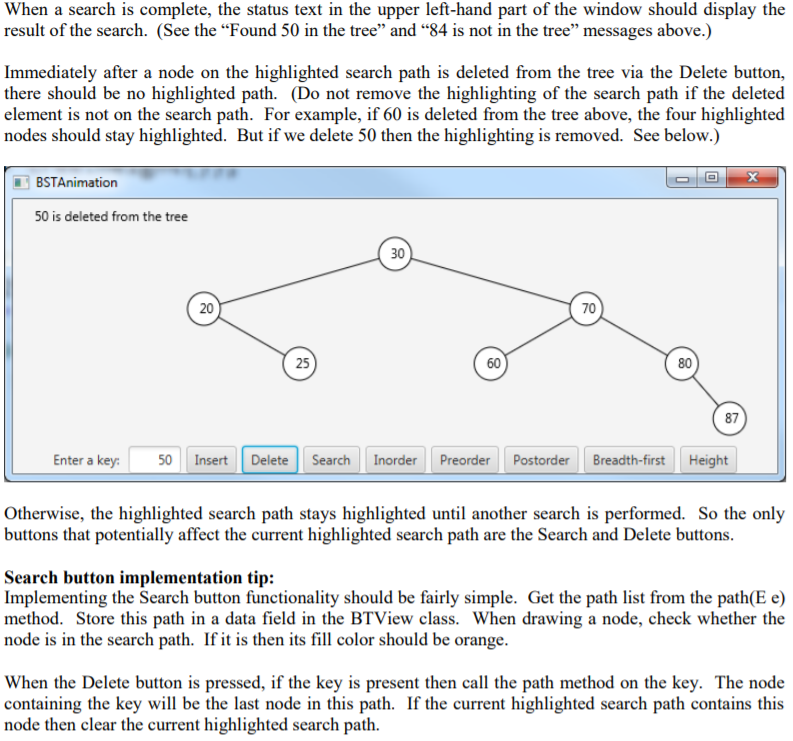
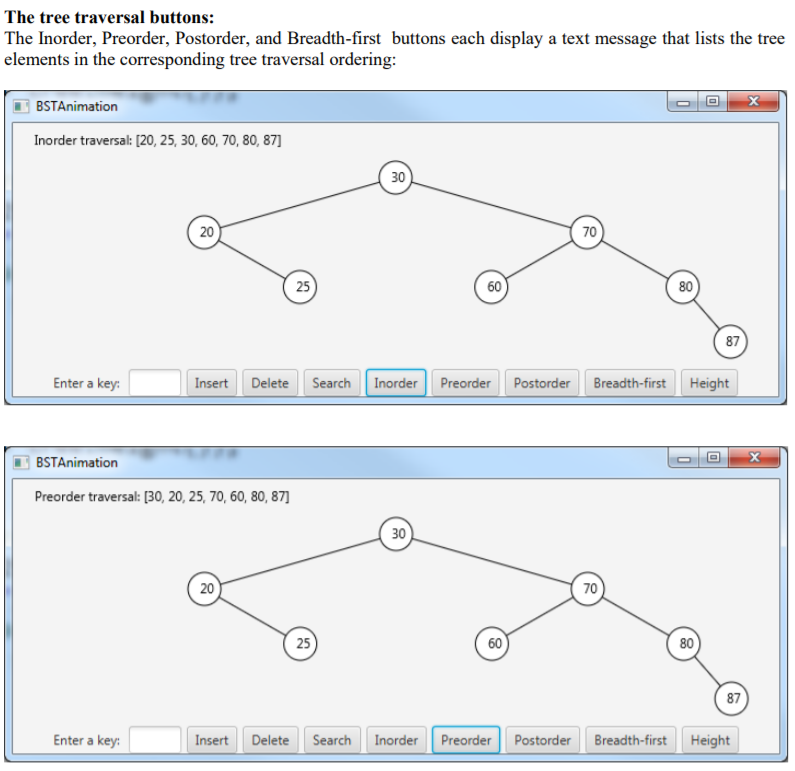
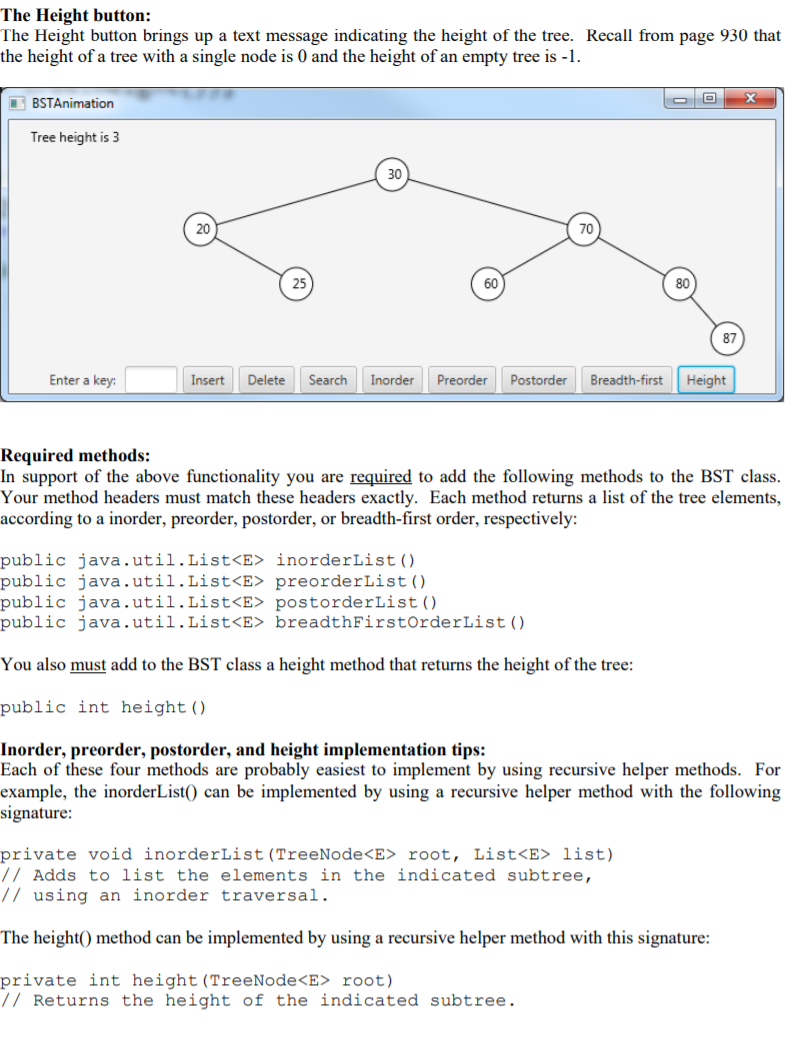
CSC 364 Homework #4 Covers: Binary search trees Instructor: Jeff Ward Worth 50 points Download the following files from Canvas: BST.java, BSTAnimation.java, BTView.java, Tree.java. The task: Modify BSTAnimation.java to add six new buttons - Search, Inorder, Preorder, Postorder, Breadth-First, and Height, along with the corresponding listener code. Widen the window so that the extra buttons fit. Add to BST.java the methods described below under "Required methods, which will support the functionality of these six buttons. Modify BTView.java so that it will display search paths. The Search button: When a user enters a key into the text box and presses the Search button, the program should shade the search path for that key. (Recall that the search path is returned by the path(E e) method, which is already provided in BST.java.) BSTAnimation Found 60 in the tree 50 20 70 30 60 80 25 87 Enter a key: 60 Insert Delete Search Inorder Preorder Postorder Breadth-first Height X BSTAnimation 84 is not in the tree 50 20 70 30 60 80 25 87 Enter a key 84 Insert Delete Search Inorder Preorder Postorder Breadth-first Height When a search is complete, the status text in the upper left-hand part of the window should display the result of the search. (See the Found 50 in the tree and 84 is not in the tree messages above.) Immediately after a node on the highlighted search path is deleted from the tree via the Delete button, there should be no highlighted path. (Do not remove the highlighting of the search path if the deleted element is not on the search path. For example, if 60 is deleted from the tree above, the four highlighted nodes should stay highlighted. But if we delete 50 then the highlighting is removed. See below.) BSTAnimation x 50 is deleted from the tree 30 20 70 25 60 80 87 Enter a key: 50 Insert Delete Search Inorder Preorder Postorder Breadth-first Height Otherwise, the highlighted search path stays highlighted until another search is performed. So the only buttons that potentially affect the current highlighted search path are the Search and Delete buttons. Search button implementation tip: Implementing the Search button functionality should be fairly simple. Get the path list from the path(E e) method. Store this path in a data field in the BTView class. When drawing a node, check whether the node is in the search path. If it is then its fill color should be orange. When the Delete button is pressed, if the key is present then call the path method on the key. The node containing the key will be the last node in this path. If the current highlighted search path contains this node then clear the current highlighted search path. The tree traversal buttons: The Inorder, Preorder, Postorder, and Breadth-first buttons each display a text message that lists the tree elements in the corresponding tree traversal ordering: BSTAnimation Inorder traversal: [20, 25, 30, 60, 70, 80, 87] 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height BSTAnimation Preorder traversal: (30, 20, 25, 70, 60, 80, 87] 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height BSTAnimation Postorder traversal: (25, 20, 60, 87, 80, 70, 30] 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height BSTAnimation Breadth-first traversal: (30, 20, 70, 25, 60, 80, 87] 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height Suggestions for implementing the traversals are provided later in this write-up. The Height button: The Height button brings up a text message indicating the height of the tree. Recall from page 930 that the height of a tree with a single node is 0 and the height of an empty tree is -1. X BSTAnimation Tree height is 3 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height Required methods: In support of the above functionality you are required to add the following methods to the BST class. Your method headers must match these headers exactly. Each method returns a list of the tree elements, according to a inorder, preorder, postorder, or breadth-first order, respectively: public java.util.List inorderList() public java.util.List preorderList() public java.util.List postorderList() public java.util.List breadthFirstOrderList() You also must add to the BST class a height method that returns the height of the tree: public int height () Inorder, preorder, postorder, and height implementation tips: Each of these four methods are probably easiest to implement by using recursive helper methods. For example, the inorderList() can be implemented by using a recursive helper method with the following signature: private void inorderList (TreeNode root, List list) // Adds to list the elements in the indicated subtree, // using an inorder traversal. The height() method can be implemented by using a recursive helper method with this signature: private int height (TreeNode root) // Returns the height of the indicated subtree. Breadth-first traversal: Breadth-first traversal may be implemented easily with a loop and a queue. The following pseudocode from Wikipedia should be useful in designing your breadthFirstOrderList code. The article refers to breadth-first order as level order. levelorder (root) q = empty queue q.enqueue (root) while not q.empty do node := q.dequeue () visit (node) if node.left # null then q.enqueue (node.left) if node.right # null then q.enqueue (node.right) What to turn in: Submit the four program files, BST.java, BSTAnimation.java, BTView.java, and Tree.java, on Canvas. You probably will not need to modify Tree.java , but you will need to modify each of the other three files. Because this is a graphical program, you will not be able to submit it to Mimir for automated grading. I will test and grade your program within a week of the due date. CSC 364 Homework #4 Covers: Binary search trees Instructor: Jeff Ward Worth 50 points Download the following files from Canvas: BST.java, BSTAnimation.java, BTView.java, Tree.java. The task: Modify BSTAnimation.java to add six new buttons - Search, Inorder, Preorder, Postorder, Breadth-First, and Height, along with the corresponding listener code. Widen the window so that the extra buttons fit. Add to BST.java the methods described below under "Required methods, which will support the functionality of these six buttons. Modify BTView.java so that it will display search paths. The Search button: When a user enters a key into the text box and presses the Search button, the program should shade the search path for that key. (Recall that the search path is returned by the path(E e) method, which is already provided in BST.java.) BSTAnimation Found 60 in the tree 50 20 70 30 60 80 25 87 Enter a key: 60 Insert Delete Search Inorder Preorder Postorder Breadth-first Height X BSTAnimation 84 is not in the tree 50 20 70 30 60 80 25 87 Enter a key 84 Insert Delete Search Inorder Preorder Postorder Breadth-first Height When a search is complete, the status text in the upper left-hand part of the window should display the result of the search. (See the Found 50 in the tree and 84 is not in the tree messages above.) Immediately after a node on the highlighted search path is deleted from the tree via the Delete button, there should be no highlighted path. (Do not remove the highlighting of the search path if the deleted element is not on the search path. For example, if 60 is deleted from the tree above, the four highlighted nodes should stay highlighted. But if we delete 50 then the highlighting is removed. See below.) BSTAnimation x 50 is deleted from the tree 30 20 70 25 60 80 87 Enter a key: 50 Insert Delete Search Inorder Preorder Postorder Breadth-first Height Otherwise, the highlighted search path stays highlighted until another search is performed. So the only buttons that potentially affect the current highlighted search path are the Search and Delete buttons. Search button implementation tip: Implementing the Search button functionality should be fairly simple. Get the path list from the path(E e) method. Store this path in a data field in the BTView class. When drawing a node, check whether the node is in the search path. If it is then its fill color should be orange. When the Delete button is pressed, if the key is present then call the path method on the key. The node containing the key will be the last node in this path. If the current highlighted search path contains this node then clear the current highlighted search path. The tree traversal buttons: The Inorder, Preorder, Postorder, and Breadth-first buttons each display a text message that lists the tree elements in the corresponding tree traversal ordering: BSTAnimation Inorder traversal: [20, 25, 30, 60, 70, 80, 87] 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height BSTAnimation Preorder traversal: (30, 20, 25, 70, 60, 80, 87] 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height BSTAnimation Postorder traversal: (25, 20, 60, 87, 80, 70, 30] 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height BSTAnimation Breadth-first traversal: (30, 20, 70, 25, 60, 80, 87] 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height Suggestions for implementing the traversals are provided later in this write-up. The Height button: The Height button brings up a text message indicating the height of the tree. Recall from page 930 that the height of a tree with a single node is 0 and the height of an empty tree is -1. X BSTAnimation Tree height is 3 30 20 70 25 60 80 87 Enter a key: Insert Delete Search Inorder Preorder Postorder Breadth-first Height Required methods: In support of the above functionality you are required to add the following methods to the BST class. Your method headers must match these headers exactly. Each method returns a list of the tree elements, according to a inorder, preorder, postorder, or breadth-first order, respectively: public java.util.List inorderList() public java.util.List preorderList() public java.util.List postorderList() public java.util.List breadthFirstOrderList() You also must add to the BST class a height method that returns the height of the tree: public int height () Inorder, preorder, postorder, and height implementation tips: Each of these four methods are probably easiest to implement by using recursive helper methods. For example, the inorderList() can be implemented by using a recursive helper method with the following signature: private void inorderList (TreeNode root, List list) // Adds to list the elements in the indicated subtree, // using an inorder traversal. The height() method can be implemented by using a recursive helper method with this signature: private int height (TreeNode root) // Returns the height of the indicated subtree. Breadth-first traversal: Breadth-first traversal may be implemented easily with a loop and a queue. The following pseudocode from Wikipedia should be useful in designing your breadthFirstOrderList code. The article refers to breadth-first order as level order. levelorder (root) q = empty queue q.enqueue (root) while not q.empty do node := q.dequeue () visit (node) if node.left # null then q.enqueue (node.left) if node.right # null then q.enqueue (node.right) What to turn in: Submit the four program files, BST.java, BSTAnimation.java, BTView.java, and Tree.java, on Canvas. You probably will not need to modify Tree.java , but you will need to modify each of the other three files. Because this is a graphical program, you will not be able to submit it to Mimir for automated grading. I will test and grade your program within a week of the due date