Build an optimization model in Excel that captures and solves the optimization problem,Thank you

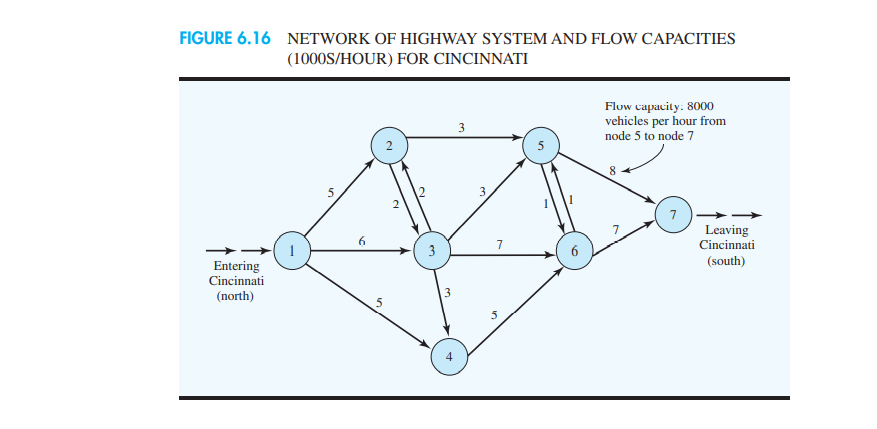
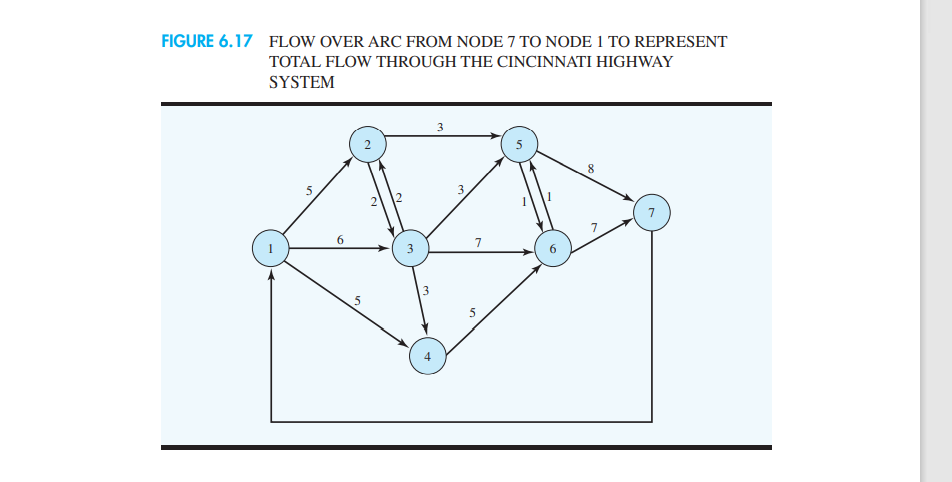
6.4 MAXIMAL FLOW PROBLEM The objective in a maximal flow problem is to determine the maximum amount of flow (vehicles, messages, fluid, etc.) that can enter and exit a network system in a given period of time. In this problem, we attempt to transmit flow through all arcs of the network as efficiently as possible. The amount of flow is limited due to capacity restrictions on the various arcs of the network. For example, highway types limit vehicle flow in a transportation system, while pipe sizes limit oil flow in an oil distribution system. The maximum or upper limit on the flow in an arc is referred to as the flow capacity of the arc. Even though we do not specify capaci- ties for the nodes, we do assume that the flow out of a node is equal to the flow into the node. As an example of the maximal flow problem, consider the north-south interstate high- way system passing through Cincinnati, Ohio. The north-south vehicle flow reaches a level of 15,000 vehicles per hour at peak times. Due to a summer highway maintenance program, which calls for the temporary closing of lanes and lower speed limits, a network of alternate routes through Cincinnati has been proposed by a transportation planning committee. The alternate routes include other highways as well as city streets. Because of differences in speed limits and traffic patterns, flow capacities vary depending on the particular streets and roads used. The proposed network with arc flow capacities is shown in Figure 6.16. The direction of flow for each are is indicated, and the are capacity is shown next to each arc. Note that most of the streets are one-way. However, a two-way street can be found between nodes 2 and 3 and between nodes 5 and 6. In both cases, the capacity is the same in each direction. We will show how to develop a capacitated transshipment model for the maximal flow problem. First, we will add an arc from node 7 back to node 1 to represent the total flow through the highway system. Figure 6.17 shows the modified network. The newly added arc shows no capacity; indeed, we will want to maximize the flow over that arc. Maximizing the flow over the arc from node 7 to node 1 is equivalent to maximizing the number of cars that can get through the north-south highway system passing through Cincinnati. The decision variables are as follows: Xjj = amount of traffic flow from node i to node j The objective function that maximizes the flow over the highway system is Max 871 FIGURE 6.16 NETWORK OF HIGHWAY SYSTEM AND FLOW CAPACITIES (1000S/HOUR) FOR CINCINNATI 3 Flow capacity. 8000 vehicles per hour from node 5 to node 7 3 7 6 1 3 7 Leaving Cincinnati (south) Entering Cincinnati (north) 5 5 4 FIGURE 6.17 FLOW OVER ARC FROM NODE 7 TO NODE 1 TO REPRESENT TOTAL FLOW THROUGH THE CINCINNATI HIGHWAY SYSTEM 3 5 8 5 7 6 3 7 4 As with all transshipment problems, each arc generates a variable and each node gener- ates a constraint. For each node, a conservation of flow constraint represents the requirement that the flow out must equal the flow in. Or, stated another way, the flow out minus the flow in must equal zero. For node 1, the flow out is X12 + x13 + X14, and the flow in is x71. There- fore, the constraint for node 1 is x12 + x13 + X14 X71 = 0 The conservation of flow constraints for the other six nodes are developed in a similar fashion. Flow Out 423 | 25 X32 + x34 + x35 + X36 X46 Node 2 Node 3 Node 4 Node 5 Node 6 Node 7 Flow In -X12 - 332 -X13 X23 0 -X14- X34 = 0 -X25 - X35 - X65 = 0 --X36 - X46 - X56 0 -X57 - X67 = 0 X56 + X57 X65 + X67 X71 Additional constraints are needed to enforce the capacities on the arcs. These 14 simple upper-bound constraints are given. X125 X136 X14 5 X232 X2553 434