Question: By recognizing each series below as a Taylor series evaluated at a particular value of , find the sum of each convergent series. A. 1

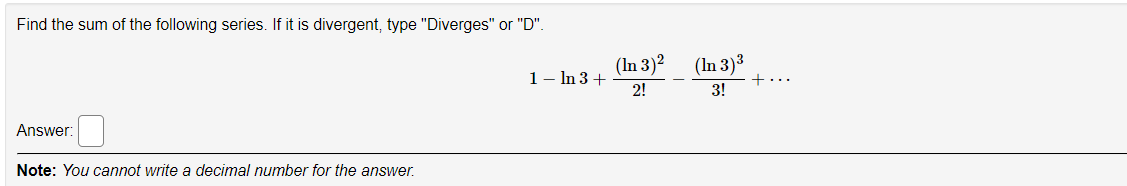
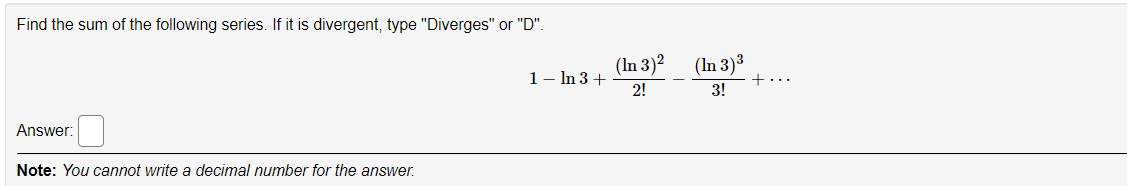
By recognizing each series below as a Taylor series evaluated at a particular value of , find the sum of each convergent series. A. 1 + 6 + + 63 64 At ... + n

+ ... + (-1)172n (2n)! + .. . =Find the sum of

By recognizing each series below as a Taylor series evaluated at a particular value of , find the sum of each convergent series. A. 1 + 6 + + 63 64 At ... + n ! + ... sin 6 B. 1 - + 74 76 of + ... + (-1)172n (2n)! + .. . =Find the sum of the following series. If it is divergent, type "Diverges" or "D". (In 3)2 (In 3)3 1 - In 3 + + .. 2! 3! Answer: Note: You cannot write a decimal number for the answer.Use sigma notation to write the Taylor series about a = co for the function. e , x0 = (-5). Taylor series =

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

6. [-/3 Points] By recognizing the series below as a Taylor series evaluated at a particular value of X, find the exact sum of the convergent series. 1+L+i+i++m+g+m 1! 2! 3! 4! n! 7. [/3 Points] By...

OO Cn (2 - 3)n Write the Taylor series for f (x ) = e about x = 3 as n=0 Find the first five coefficients. CO= S1= C2= C3= C4=By recognizing each series below as a Taylor series evaluated at a...

By recognizing each series below as a Taylor series evaluated at a particular value of x , find the sum of each convergent series. A . 1 - 2 2 2 ! + 2 4 4 ! - 2 6 6 ! + cdots + ( - 1 ) n 2 2 n ( 2 n...

By recognizing each series below as a Taylor series evaluated at a particular value of x, find the sum of each convergent series. A. 1 + + ( ) 2 + () + () + + () + : B. 1+7+ +

By recognizing each series below as a Taylor series evaluated at a particular value of x find the sum of each convergent series A 1 3 31 31 3 7 B 3 1 72 272 1 1 ng2n 1 2n 1 M

(20 points) By recognizing each series below as a Taylor series evaluated at a particular value of x, find the sum of each convergent series. A. 1+21+(21)2+(21)3+(21)4++(21)n+= B....

By recognizing each series below as a Taylor series evaluated at a particular value of x, find the sum of each convergent series. A. 1 + 2 + ( 2 ) 2 + ( 2 ) 3 + ( # ) + + ... + ( 2 ) *2 + ... = B. 1...

(1 point) By recognizing each series below as a Taylor series evaluated at a particular value of x, find the sum of each convergent series. A. 1+7+ 72 + 74 2! 3 ! 4! + ... + n! B. 1 - 72 +... +...

please explain (1 point) By recognizing each series below as a Taylor series evaluated at a particular value of x, find the sum of each convergent series. A. 4 - + 4' 3 ! + ... + (1)42n+1 5! 71...

Ch 10 Approximating Functions Using Series 10.2 Taylor Series Please show work and answer with it 36 1296 By recognizing the series 1 - (-1) " (6) 2n + +. . . as 2! 4! (2n)! a Taylor series evaluated...

When UV light of wavelength 285nm falls on a metal surface, the maximum kinetic energy of emitted electrons is 1.40eV. What is the work function of the metal?

Suppose you have a project that will produce a single widget. Widgets today cost $1 and the project costs $0.90. The risk-free rate is 5%. Under what circumstances would you invest immediately in the...

Find the following indefinite integrals: 1 x 2 + 7 x + 6 d x = 8 x + 1 x 2 + 7 x + 6 d x = Show all images Show all images Show all images done loading

Elvin, a single taxpayer 45 years of age, sells his residence in 2016. He receives $35,000 in cash, and the buyer assumes his $100,000 mortgage. Elvin also pays $8,100 in commissions and transfer...

Loran Inc. had the following equivalent units schedule and cost for its fabrication department during the month of September: Required: 1. Calculate the unit cost for materials, for conversion, and...

W Promotions sells T-shirts imprinted with high school names and logos. Last year the shirts sold for $18 each, and variable costs were $5.40 per shirt. At this cost structure, the breakeven point...

Victoria Ephanor manages a small product distribution company. Because the business is growing fast, Ephanor recognizes that it is time to manage the vast information pool to help guide the...

Inc. prepared the following cash budget for the fourth quarter. Required Fill in the missing amounts, assuming that Topper desires to maintain a $15,000 minimum monthly cash balance. Any required...

Please help it's urgent thank you. please write 400-450 words. thank you QUESTION 4 (20 MARKS) The success of any project is dependent on a diverse range of skills, abilities and competencies of the...

2. We can change the use and meaning of the concepts and thereby the meaning of the social reality to which they refer.

3. What does it mean when we say that we attribute a certain meaning to our experiences?

2. In this chapter, the reader should reflect on the following concepts : Thomas theorem, premise of action, utterance and mental constructions.