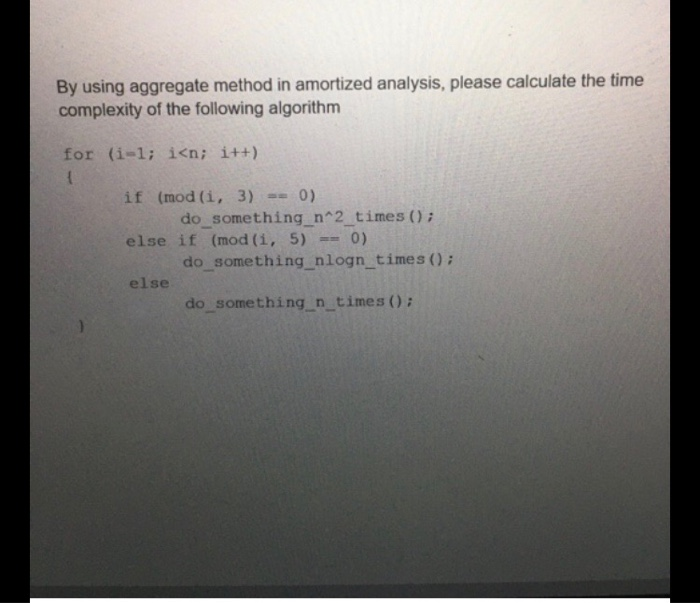
By using aggregate method in amortized analysis, please calculate the time complexity of the following algorithm for (i-1; i Task 2: Christmas Lights-15 Consider that you have a set of N Christmas lights, which can turn red or green. The lights are numbered from 1 to N. Initially at time step 1 they are all red. The mechanism is set such that at time t, all lights whose id is divisible by t will change color (i.e. red to green, or green to red). For example, given 6 lights, numbered 1,2,3,4,5,6 at time step 1 RRRRRR at time step 2 at time step 3 RGRGRG RGGGRR How many lights will be red at the end of N time steps? Give a pseudocode of your algorithm and its complexity. If the algorithm complexity is O(n) then you get 5 points If the algorithm complexity is O(n) then you get 10 points If the algorithm complexity is less than O(n) then you get 15 points