Question: (c) (5 points) Let the cost function to minimize is: J(w)=i=1n(yiTxi))2+j=0dj2 Prove that the vector w that minimizes J(w) is: w=(XX+I)1Xy where X is the

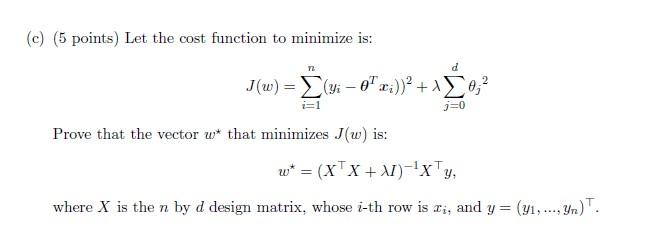
(c) (5 points) Let the cost function to minimize is: J(w)=i=1n(yiTxi))2+j=0dj2 Prove that the vector w that minimizes J(w) is: w=(XX+I)1Xy where X is the n by d design matrix, whose i-th row is xi, and y=(y1,,yn). (c) (5 points) Let the cost function to minimize is: J(w)=i=1n(yiTxi))2+j=0dj2 Prove that the vector w that minimizes J(w) is: w=(XX+I)1Xy where X is the n by d design matrix, whose i-th row is xi, and y=(y1,,yn)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

File Home Insert Page Layout Formulas Data Review View Help Search A1 x A B C D Chapter 7-Master it! In practice, the use of the dividend discount model is refined from the method we presented in...

Supply Chain Management Introduction Outline What is supply chain management? Significance of supply chain management. Push vs. Pull processes utdallas.edu/~metin 1 A Generic Supply Chain Sources:...

Submitted to Management Science manuscript MS-0001-1922.65 Authors are encouraged to submit new papers to INFORMS journals by means of a style file template, which includes the journal title....

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

re Regular Languages and Finite Automata (a) Let L be the set of all strings over the alphabet {a, b} that end in a and do not contain the substring bb. Describe a deterministic finite automaton...

8.1 WRITE on paper for upvote. Section: 25, 32, 33 please 8.1 General Linear Transformations 20. Consider the basis S = {V1, V2} for R', where v, = (-2, 1) and 9. T : Rx - R., where V2 = (1, 3), and...

350 Specification and Verification II Explain how a register can be modelled either as a unit-delay, or with an explicit clock input. [4 marks] Describe the relationship between the two models. [4...

Answer the questions. in the following attachments. Question 1. (10 marks) Consider the function z = f(x, y) = x/y. Showing all steps, use the Newton Quotient approach to find ?z/?y. Question 2. (5...

Book: Facilities Planning 4th Edition You are given the following layout consisting of 6 departments. The total layout is 60x30 in size (so each square is 10x10). Interior lines are just to indicate...

tax Consider the market for apple juice. In this market, the supply curve is given by QS = 10PJ 5PA and the demand curve is given by QD = 100 15PJ + 10PT , where J denotes apple juice, A denotes...

: (i) What data structures are maintained by the page manager. (ii) What happens when a machine performs a read operation to a page. (iii) What happens when a machine performs a write operation to a...

Cincinnati Painting Service Inc. specializes in painting houses. During June, its first month of operations, Cincinnati Painting engaged in the following transactions: June 1 Issued common stock for...

Investigate LEED (Leadership in energy and Environmental Design) building designs. Should all new buildings be required by law to adopt LEED design standards and conform to the LEED rating system?...

Assume that Adams industries holds 5 7 , 0 0 0 shares of FedEx common stock, which is not a liage enough ownership interest to allow Adams to exercise significant influence over Fectex. On December 3...

When older adults have difficulty with transportation and communication, or may be reluctant to request needed assistance to which they are entitled, they may be in need of: Group of answer choices...