C++ code for a number's game

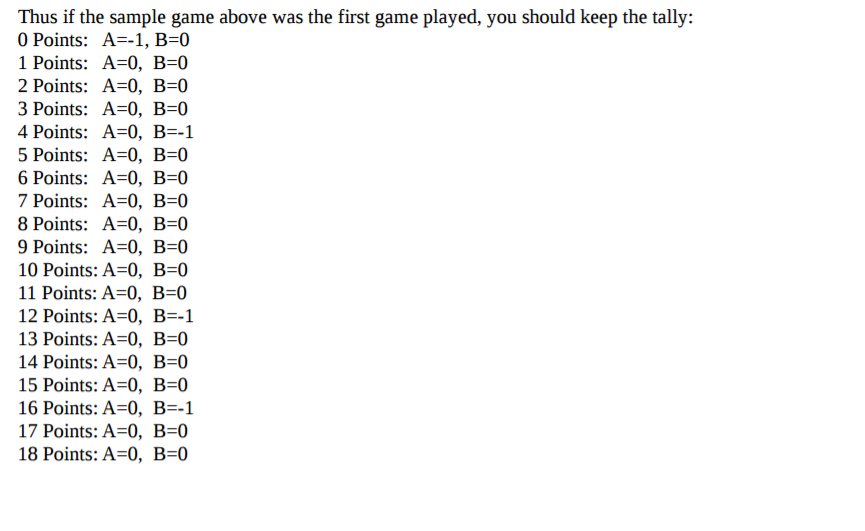
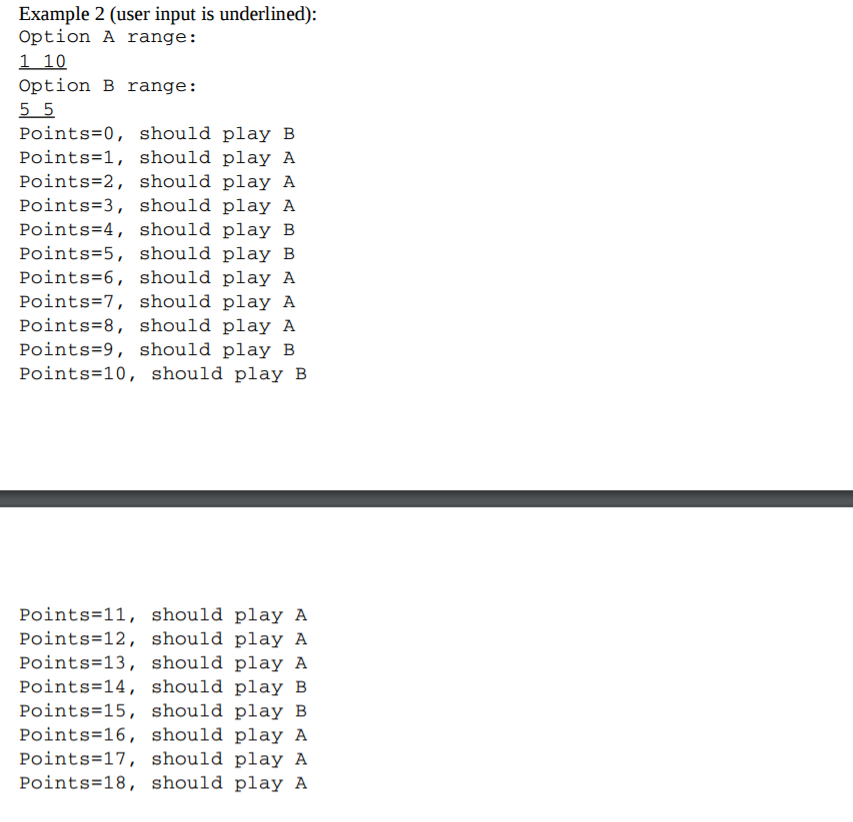
Suppose there is a game with two options: A and B. Each of these options adds a different amount of points from a range of numbers. You start with 0 points and your goal is to reach 19 or 20 points. For example, suppose you had the following options: A number between 4 through 7. B -number between 1 through 8. A sample game might go: Points -0, choose option A(add 4-7). Points 4, choose option B(add 1-8). Points 12, choose option B(add 1-8). Points 16, choose option B(add 1-80. Points 21, you lose. Make a program that asks the user to give the ranges for both options A and B. You may assume that both options A and B have a minimum of adding at least one point. To figure out which moves are the best, simulate 10,000,000 games (this should take about 5 seconds to run) with random choices at each turn. Record how often you won/lost the game for each point value and each option picked. If you won the game, each point/option along the whole game should get a +1 and each loss a -1. Suppose there is a game with two options: A and B. Each of these options adds a different amount of points from a range of numbers. You start with 0 points and your goal is to reach 19 or 20 points. For example, suppose you had the following options: A number between 4 through 7. B -number between 1 through 8. A sample game might go: Points -0, choose option A(add 4-7). Points 4, choose option B(add 1-8). Points 12, choose option B(add 1-8). Points 16, choose option B(add 1-80. Points 21, you lose. Make a program that asks the user to give the ranges for both options A and B. You may assume that both options A and B have a minimum of adding at least one point. To figure out which moves are the best, simulate 10,000,000 games (this should take about 5 seconds to run) with random choices at each turn. Record how often you won/lost the game for each point value and each option picked. If you won the game, each point/option along the whole game should get a +1 and each loss a -1