C++ Coding

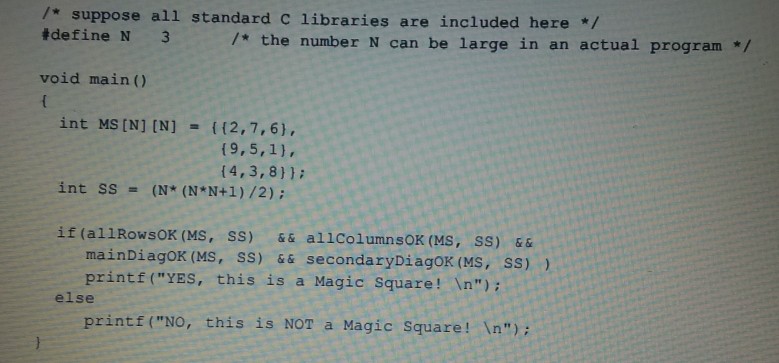
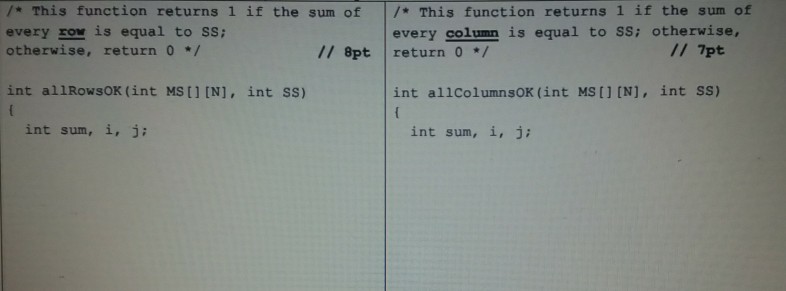
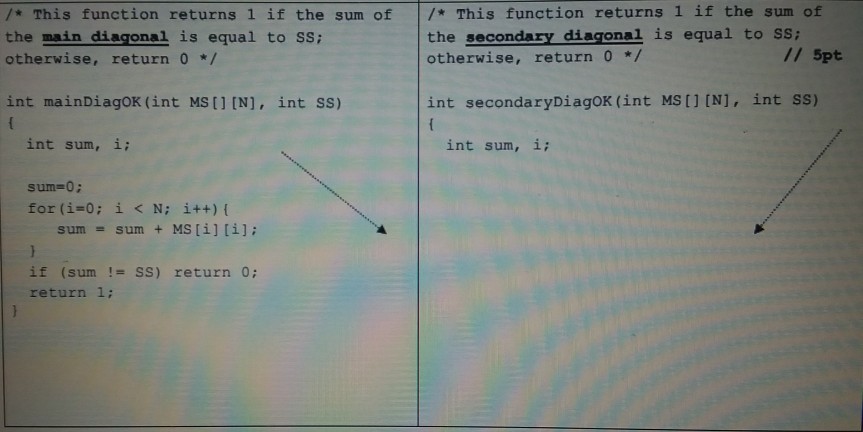
(20 pt) Recall the Sudoku puzzle that you studied in Assignment 1. In this question, you will work on a similar number placement puzzle known as Magic Square (MS). Here is the description from the webl A magic square is an arrangement of dist integer numbers (i.e., each number is used once) from 1 to N2 in an NxN square grid, where the numbers in each row, and in each column, and the numbers in the maln and secondary diagonals, all add up to the same number, which is N'(N2+ 1)/2. For example, we can place the numbers from 1 to 9 32 on a 3x3 MS with the same sum of 15, and place the numbers from 1 to 25-52 on a 5x5 MS with the same sum of 65, as shown in the below figures. 23 619 2 15 4 12 25 816 9 5 1-15 118 1 14 22 4 3 8 15 11 24 7 203 15 15 15 15 15 17 5 13 21 9 Suppose we are interested in checking ifa given int MS [N] [N] {{/*initial values /, is a valid Magic Square or not. Also suppose we have the four helper functions in the next page that respectively check if the sum of the numbers in each row, and in each column, and in the main and secondary diagonals are all equal to the same sum (SS) N (N + 1)/2. Then we can simply check if a given MS [N] [N] is a valid Magic Square or not as follows: (20 pt) Recall the Sudoku puzzle that you studied in Assignment 1. In this question, you will work on a similar number placement puzzle known as Magic Square (MS). Here is the description from the webl A magic square is an arrangement of dist integer numbers (i.e., each number is used once) from 1 to N2 in an NxN square grid, where the numbers in each row, and in each column, and the numbers in the maln and secondary diagonals, all add up to the same number, which is N'(N2+ 1)/2. For example, we can place the numbers from 1 to 9 32 on a 3x3 MS with the same sum of 15, and place the numbers from 1 to 25-52 on a 5x5 MS with the same sum of 65, as shown in the below figures. 23 619 2 15 4 12 25 816 9 5 1-15 118 1 14 22 4 3 8 15 11 24 7 203 15 15 15 15 15 17 5 13 21 9 Suppose we are interested in checking ifa given int MS [N] [N] {{/*initial values /, is a valid Magic Square or not. Also suppose we have the four helper functions in the next page that respectively check if the sum of the numbers in each row, and in each column, and in the main and secondary diagonals are all equal to the same sum (SS) N (N + 1)/2. Then we can simply check if a given MS [N] [N] is a valid Magic Square or not as follows