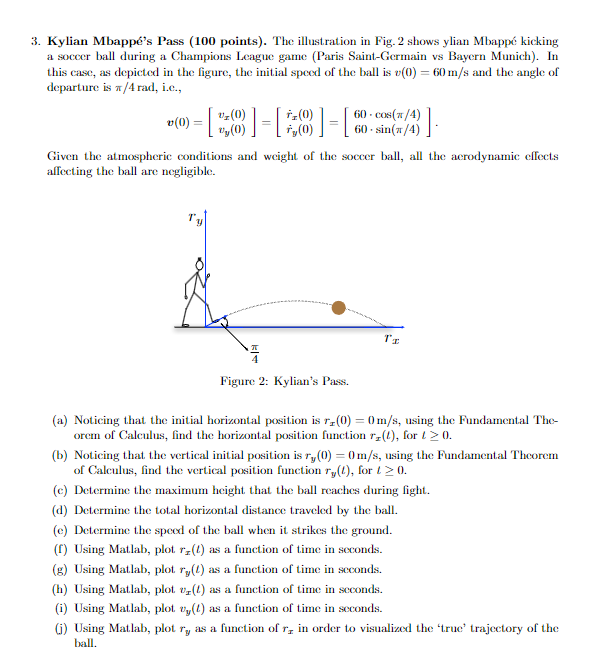
2. Circular Path (210 points). The illustration in Fig. 1(a) shows a small ball traveling along a circular path with an instantaneous angular velocity (t) and an instantaneous angular acceler- ation (1). The radius of the circumference described by the trajectory of the ball is ro and the instantaneous angle (t) is measured from the horizontal line that intersects the center of the circle, as depicted in Fig. 1(a). In this case, the angular acceleration is given by the function (t)=sint rad/s, for all > 0, = where the corresponding initial conditions are 0(0) 1 rad/s and (0) = 0 rad. In this case, obviously, the instantaneous position of the ball from the center of the circle remains constant. Specifically, r() ro = 1 m. Consistently with the previous definitions, r(t) and (t) are the polar coordinates used to describe the kinematics of the system. As shown in Fig. 1(b), the instantaneous radial direction is represented using the unit vector u,(t) and the transversal direction is represented using the unit vector uo(!). Also, as shown in Fig. 1(b), the instantaneous tangential and normal directions along the trajectory of the ball are represented using the unit vectors u(t) and un(t), respectively. (a) Consider Fig. 1(b) and show mathematically that u,(t) = cos|0 (1)]i + sin[0(1)]j- (b) Consider Fig. 1(b) and show mathematically that uo(!)=sin(t)]i + cos[0(1)\j. s(t)-ro(t) 0,0 (a) (b) 0 247 (c) Consider Fig. 1(b) and show mathematically that u(t) = u(t). (d) Consider Fig. 1(b) and show mathematically that un(t) = -u,(t). (e) Using the chain rule, show mathematically that u,(t) = (t)u(t). (f) Using the chain rule, show mathematically that (t) = (t)u(t). (g) Using the Fundamental Theorem of Calculus (FTC) and the initial condition (0) = 1 rad/s, find (+) for t> 0. (h) Using the Fundamental Theorem of Calculus (FTC) and the initial condition 0(0) = 0 rad, find (t) for t 0. Write the position vector of the moving ball, using polar coordinates. (j) Determine the radial component of the velocity vector (when written using polar coo dinates). (k) Determine the transverse component of the velocity vector (when written using polar coordinates). (1) Determine the radial component of the acceleration vector (when written using polar coordinates). (m) Determine the transverse component of the acceleration vector (when written using polar coordinates). (n) Explain, using simple algebraic and geometrical arguments, that the scalar distance-travelled function s(t) is given by s(t) = roo(t). 3. Kylian Mbapp's Pass (100 points). The illustration in Fig. 2 shows ylian Mbapp kicking a soccer ball during a Champions League game (Paris Saint-Germain vs Bayern Munich). In this case, as depicted in the figure, the initial speed of the ball is v(0) = 60 m/s and the angle of departure is x/4 rad, i.c., Uz (0) tz(0) fy(0) = 60. cos(x/4) 60+ sin(x/4) 3] Given the atmospheric conditions and weight of the soccer ball, all the aerodynamic effects affecting the ball are negligible. TI Figure 2: Kylian's Pass. (a) Noticing that the initial horizontal position is r,(0) = 0 m/s, using the Fundamental The- orem of Calculus, find the horizontal position function rx(t), for t 0. (b) Noticing that the vertical initial position is r,(0) = 0 m/s, using the Fundamental Theorem of Calculus, find the vertical position function ry(t), for > 0. (c) Determine the maximum height that the ball reaches during fight. (d) Determine the total horizontal distance traveled by the ball. (e) Determine the speed of the ball when it strikes the ground. (f) Using Matlab, plot r() as a function of time in seconds. (g) Using Matlab, plot ry(t) as a function of time in seconds. (h) Using Matlab, plot v(t) as a function of time in seconds. (i) Using Matlab, plot vy(!) as a function of time in seconds. (i) Using Matlab, plot ry as a function of r in order to visualized the 'true' trajectory of the ball. (o) Using the relationship s(t) = ro(t), find the instantaneous speed of the ball, v(t) = s(t), as a function of (t). (p) Determine the tangential component of the velocity vector (when written using tangential- and-normal coordinates). (q) Determine the normal component of the velocity vector (when written using tangential- and-normal coordinates). (r) Determine the tangential component of the acceleration vector (when written using tangential-and-normal coordinates). (s) Determine the normal component of the acceleration vector (when written using tangential- and-normal coordinates). (t) What is the instantaneous velocity vector in polar coordinates at time t = 1s? (u) What is the instantaneous velocity vector in tangential-and-normal coordinates at time t = 1s?