C++

Design and construct a computer program in C++ that will illustrate the effects of rounding errors and truncation errors. Be sure to follow the documentation and programming style policies of the Computer Science Department. Also, note that the arguments of all trigonometric functions in this course are measured in radians.

he following is a plot of the function f(x) = x² - sin(2 x²) - 1 :

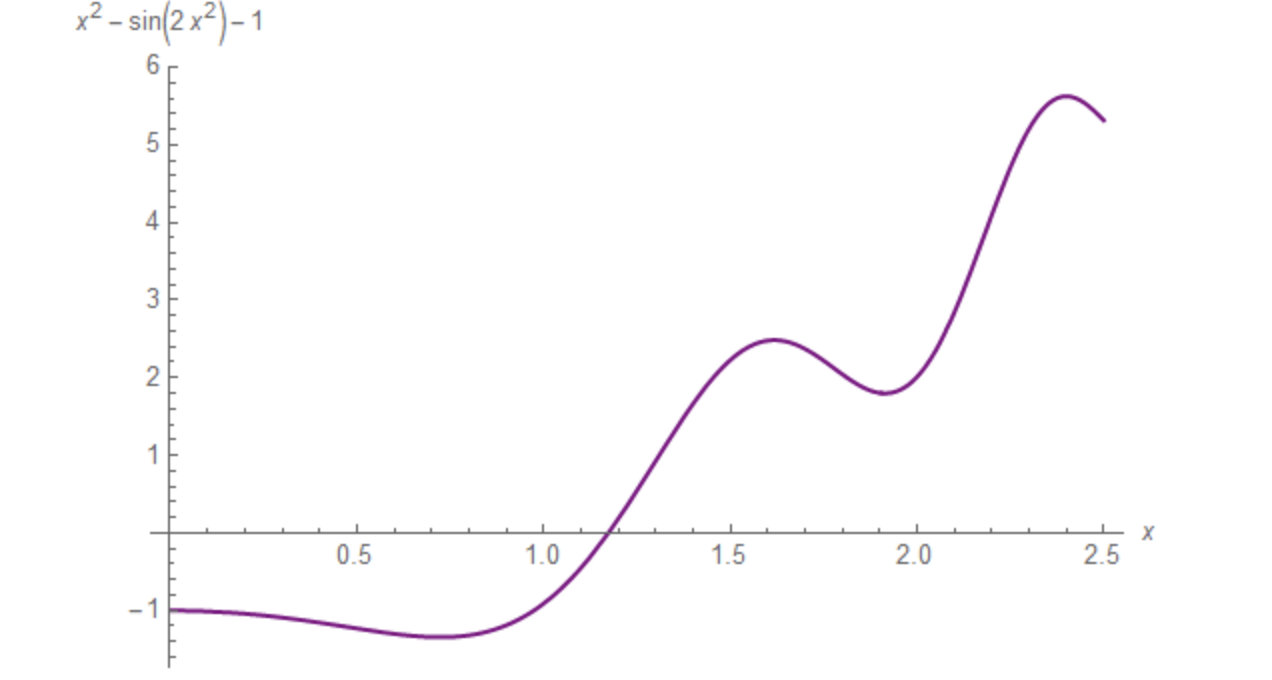
In order to illustrate the effects of the two major error sources, rounding and truncation, attempt to determine an approximation to the derivative of f(x) at x = 2.0 radians using the difference approximation given below. (The true answer is 4 - 8 cos(8) or about 5.1640002704689082070).

Use the formula:

f'(x) (f(x+h) - f(x)) / h

with h=1, 0.5, 0.25, ... 1.8189894035459e-12

(i.e., keep halving h 39 times or until it is less than 2.0e-12.)

Neatly print out the values of i, h, your approximation to f'(x), and the error in the approximation for each value of h used. The value of i is just the loop index and you may omit it, if you like. This error will include the effects of both truncation and rounding. An example of how your output might be organized:

i h approx error 0 1.000000e+000 x.xxxxxxe+000 -y.yyyyyye+000 1 5.000000e-001 -x.xxxxxxe+000 y.yyyyyye-001 ... ...

Write down (in your output file or in another file submitted with your program) any conclusions that you can make from these experiments.

x- sin(2x2)-1 6 5 4 3 2 N 1 0.5 1.0 1.5 2 2.0 L X 2.5 - 1