Question: c) For f ( x) = x - 4x over the interval [-2,1] , show that f (x) satisfies the hypothesis of the Mean Value
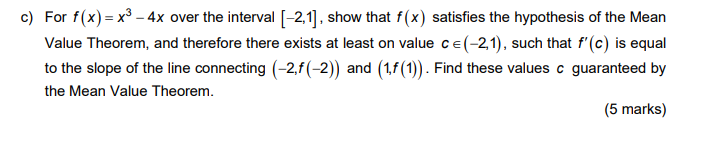
![interval [-2,1] , show that f (x) satisfies the hypothesis of the](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679e1bf9abd5_6796679e1bf88948.jpg)
c) For f ( x) = x - 4x over the interval [-2,1] , show that f (x) satisfies the hypothesis of the Mean Value Theorem, and therefore there exists at least on value ce (-2,1), such that f'(c ) is equal to the slope of the line connecting (-2.f (-2)) and (1,f (1)) . Find these values c guaranteed by the Mean Value Theorem
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


