C++ Help

Consider an array-based implementation of a binary search tree bst. Figure 16-1 presents such a representation for a particular binary search tree.

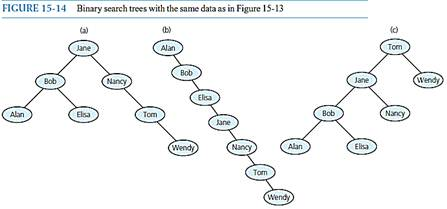
a. Depict the array in an array-based implementation for the binary search tree in Figure 15 - 14a of Chapter 15. Assume that tree items are strings.

b. Show the effect of each of the following sequential operations on the array in part a of this exercise.

bst.add("Doug");

bst.remove("Nancy");

bst.remove("Bob");

bst.add("Sarah");

c. Repeat parts a and b of this exercise for the tree in Figure 15-14c.

d. Write an inorder traversal algorith, for this array-based implementation.

*************************

PriorityQueueInterface.h

*************************

/** @file PriorityQueueInterface.h */

#ifndef PRIORITY_QUEUE_INTERFACE_ #define PRIORITY_QUEUE_INTERFACE_

template class PriorityQueueInterface

{ public: /** Sees whether this priority queue is empty. @return True if the priority queue is empty, or false if not. */ virtual bool isEmpty() const = 0; /** Adds a new entry to this priority queue. @post If the operation was successful, newEntry is in the priority queue. @param newEntry The object to be added as a new entry. @return True if the addition is successful or false if not. */ virtual bool enqueue(const ItemType& newEntry) = 0; /** Removes from this priority queue the entry having the highest priority. @post If the operation was successful, the highest priority entry has been removed. @return True if the removal is successful or false if not. */ virtual bool dequeue() = 0; /** Returns the highest-priority entry in this priority queue. @pre The priority queue is not empty. @post The highest-priority entry has been returned, and the priority queue is unchanged. @return The highest-priority entry. */ virtual ItemType peek() const = 0; /** Destroys object and frees memory allocated by object. */ virtual ~PriorityQueueInterface() { } }; // end PriorityQueueInterface #endif

FIGURE 15-14 Binary search trees with the same data as in Fiure 15-13 (d Alan Tom Bob Bob tendy Elea Tom Bob Nancy ane Wendy Alan Elra Tom Wendy