Question: C++ Implement the Newton's method (xo = 1) and Secant Algorithm (x_1 = 0.1, Xo = 1) in C++ to solve an arbitrary nonlinear function

C++ Implement the Newton's method (xo = 1) and Secant Algorithm (x_1 C++

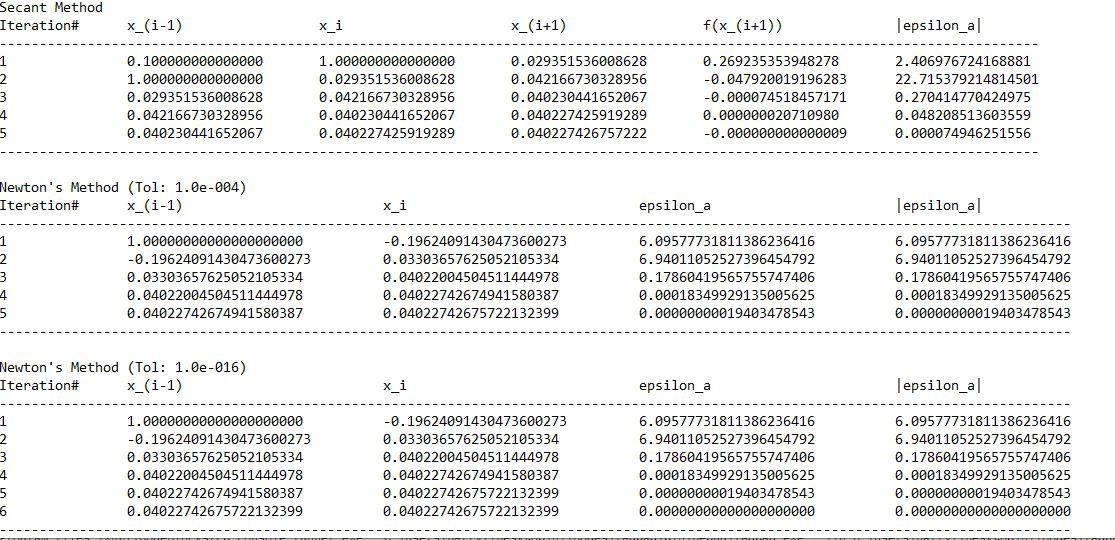
= 0.1, Xo = 1) in C++ to solve an arbitrary nonlinear

Implement the Newton's method (xo = 1) and Secant Algorithm (x_1 = 0.1, Xo = 1) in C++ to solve an arbitrary nonlinear function (find its zero(s)). The target function can be defined as anonymous, inline or a file. Stop condition: (1) The maximum n-iterations = 1000 (2) For Newton's method: 5104,10-16 For Secant Method: Significant digit = 3. Testing data: Try this function 3x? sin x +et 25x and report the results. Output: (1) For Secant method, your program should print all intermediate results following this format: Iteration# Xi-1 X; f(x+1) & (2) For Newton' Method, your program should print all intermediate results following this format: Xitl Iteration# Xi-1 X; Ea Secant Method Iteration# x_(i-1) x_i x_(i+1) f(x_(i+1)) Tepsilon_al 1 2 3 4 5 0.100000000000000 1.000000000000000 0.029351536008628 0.042166730328956 0.040230441652067 1.000000000000000 0.029351536008628 0.042166730328956 0.040230441652067 0.040227425919289 0.029351536008628 0.042166730328956 0.040230441652067 0.040227425919289 0.040227426757222 0.269235353948278 -0.047920019196283 -0.000074518457171 0.000000020710980 -0.000000000000009 2.406976724168881 22.715379214814501 0.270414770424975 0.048208513603559 0.000074946251556 Newton's Method (Tol: 1.0e-004) Iteration# x_(i-1) x_i epsilon_a Tepsilon_al 1 2 3 4 5 1.00000000000000000000 -0.19624091430473600273 0.03303657625052105334 0.04022004504511444978 0.04022742674941580387 -0.19624091430473600273 0.03303657625052105334 0.04022004504511444978 0.04022742674941580387 0.04022742675722132399 6.09577731811386236416 6.94011052527396454792 0.17860419565755747406 0.00018349929135005625 0.00000000019403478543 6.09577731811386236416 6.94011052527396454792 0.17860419565755747406 0.00018349929135005625 0.00000000019403478543 Newton's Method (Tol: 1.0-016) Iteration x_(i-1) x_i epsilon_a Tepsilon_al 1 2 3 4 1.00000000000000000000 -0.19624091430473600273 0.03303657625052105334 0.04022004504511444978 0.04022742674941580387 0.04022742675722132399 -0.19624091430473600273 0.03303657625052105334 0.04022004504511444978 0.04022742674941580387 0.04022742675722132399 0.04022742675722132399 6.09577731811386236416 6.94011052527396454792 0.17860419565755747406 0.00018349929135005625 0.00000000019403478543 0.00000000000000000000 6.09577731811386236416 6.94011052527396454792 0.17860419565755747406 0.00018349929135005625 0.00000000019403478543 0.00000000000000000000 6 Implement the Newton's method (xo = 1) and Secant Algorithm (x_1 = 0.1, Xo = 1) in C++ to solve an arbitrary nonlinear function (find its zero(s)). The target function can be defined as anonymous, inline or a file. Stop condition: (1) The maximum n-iterations = 1000 (2) For Newton's method: 5104,10-16 For Secant Method: Significant digit = 3. Testing data: Try this function 3x? sin x +et 25x and report the results. Output: (1) For Secant method, your program should print all intermediate results following this format: Iteration# Xi-1 X; f(x+1) & (2) For Newton' Method, your program should print all intermediate results following this format: Xitl Iteration# Xi-1 X; Ea Secant Method Iteration# x_(i-1) x_i x_(i+1) f(x_(i+1)) Tepsilon_al 1 2 3 4 5 0.100000000000000 1.000000000000000 0.029351536008628 0.042166730328956 0.040230441652067 1.000000000000000 0.029351536008628 0.042166730328956 0.040230441652067 0.040227425919289 0.029351536008628 0.042166730328956 0.040230441652067 0.040227425919289 0.040227426757222 0.269235353948278 -0.047920019196283 -0.000074518457171 0.000000020710980 -0.000000000000009 2.406976724168881 22.715379214814501 0.270414770424975 0.048208513603559 0.000074946251556 Newton's Method (Tol: 1.0e-004) Iteration# x_(i-1) x_i epsilon_a Tepsilon_al 1 2 3 4 5 1.00000000000000000000 -0.19624091430473600273 0.03303657625052105334 0.04022004504511444978 0.04022742674941580387 -0.19624091430473600273 0.03303657625052105334 0.04022004504511444978 0.04022742674941580387 0.04022742675722132399 6.09577731811386236416 6.94011052527396454792 0.17860419565755747406 0.00018349929135005625 0.00000000019403478543 6.09577731811386236416 6.94011052527396454792 0.17860419565755747406 0.00018349929135005625 0.00000000019403478543 Newton's Method (Tol: 1.0-016) Iteration x_(i-1) x_i epsilon_a Tepsilon_al 1 2 3 4 1.00000000000000000000 -0.19624091430473600273 0.03303657625052105334 0.04022004504511444978 0.04022742674941580387 0.04022742675722132399 -0.19624091430473600273 0.03303657625052105334 0.04022004504511444978 0.04022742674941580387 0.04022742675722132399 0.04022742675722132399 6.09577731811386236416 6.94011052527396454792 0.17860419565755747406 0.00018349929135005625 0.00000000019403478543 0.00000000000000000000 6.09577731811386236416 6.94011052527396454792 0.17860419565755747406 0.00018349929135005625 0.00000000019403478543 0.00000000000000000000 6

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Please write a C++ program. Programming tasks Your main programming task is to implement a nonlinear solver class with appropriate methods. The class should be able to solve using single and double...

MGHW5 for info; Bisection Method: Newton's Method: Secant method: This assignment deals with root-finding algorithms and should be done using the code from MGHW5. It is recommended that you take the...

I need help what am I doing wrong in my matlab code that isn't aligned with the instructions? first 4 photos are the instructions and the ones after are my matlab code. Instructions: You will write a...

C++ Implement the Newton's method (Xo = 1) and Secant Algorithm (x_1 = 0.1, xo = 1) in C++ to solve an arbitrary nonlinear function (find its zero(s)). The target function can be defined as...

nodes, but at least its bias can be quantified by Markov Chain L. INTRODUCTION analysis and thus can be corrected via appropriate re-weighting The popularity of online social networks (OSNs) in...

MGHW5: Bisection Method: Newton's Method: Secant Merhod: This assignment deals with root-finding algorithms and should be done using the code from MGHW5. It is recommended that you take the following...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

MGHW5 for more info: Bisection Method: Newton's Method: Secant method: This assignment deals with root-finding algorithms and should be done using the code from MGHW5. It is recommended that you take...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

Exxon Co purchased a new natural gas deposit for $3M. Exxon believes they can extract 1.5 million cubic feet of natural gas. In year 1, they extracted 500,000 cubic feet of natural gas and sold...

The U.S. airline industry has long struggled to make a profit. Analysts point to a number of factors that have made the industry a difficult place in which to do business. Over the years, larger...

Are there business processes that do not in some way affect accounting records or financial statements? Briefly describe the five components of an accounting information system. Describe how sales...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

12-12 With three or four of your classmates, select a sport, such as football, baseball, basketball, or soccer. Use the web to research how the sport uses data and analytics to improve team...

12-13 How is GE changing its business strategy and business model? What is the role of information technology in GEs business?

Are there any times of day when purchases are most common? Do people buy more products while at work (likely during the day) or at home (likely in the evening)?