c. Obtain the probability that the sampling error made in estimating the population mean length of stay by the mean length of stay of a sample of 84 patients will be at most 2 days.

The probability is approximately?

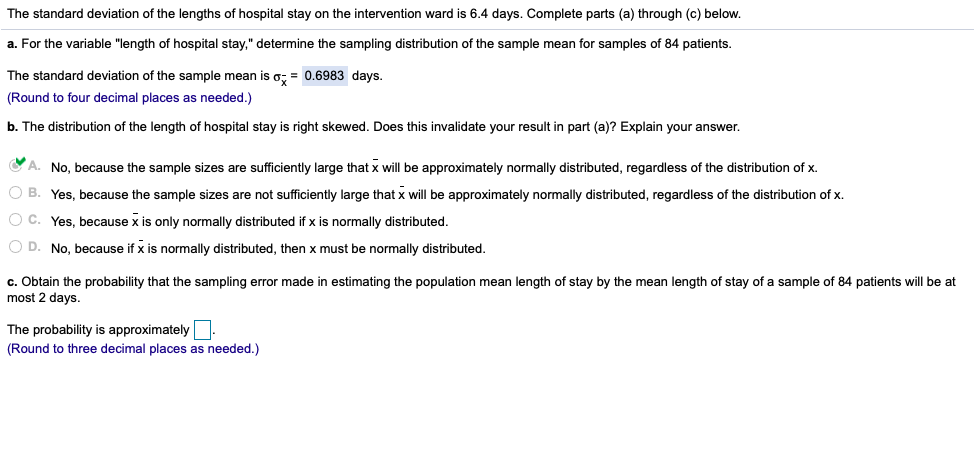
The standard deviation of the lengths of hospital stay on the intervention ward is 6.4 days. Complete parts (a) through (c) below. a. For the variable "length of hospital stay," determine the sampling distribution of the sample mean for samples of 84 patients. The standard deviation of the sample mean is of = 0.6983 days. (Round to four decimal places as needed.) b. The distribution of the length of hospital stay is right skewed. Does this invalidate your result in part (a)? Explain your answer. O A. No, because the sample sizes are sufficiently large that x will be approximately normally distributed, regardless of the distribution of x. O B. Yes, because the sample sizes are not sufficiently large that x will be approximately normally distributed, regardless of the distribution of x. O C. Yes, because x is only normally distributed if x is normally distributed. O D. No, because if x is normally distributed, then x must be normally distributed. c. Obtain the probability that the sampling error made in estimating the population mean length of stay by the mean length of stay of a sample of 84 patients will be at most 2 days. The probability is approximately|]. (Round to three decimal places as needed.)