(C++ please help)

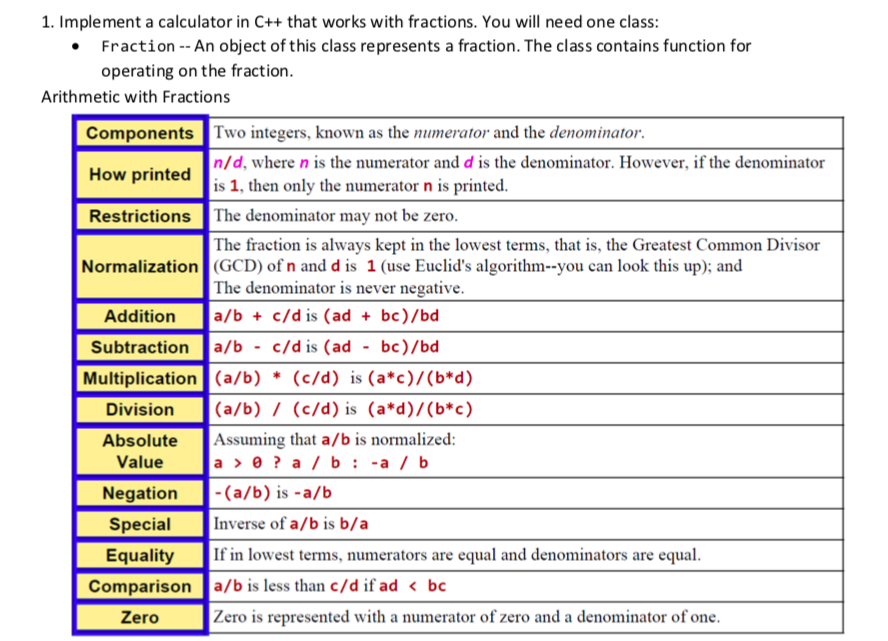
1. Implement a calculator in C++ that works with fractions. You will need one class: Fraction - An object of this class represents a fraction. The class contains function for operating on the fraction. . Arithmetic with Fractions Components Two integers, known as the numerator and the denominator. How printed Restrictions The denominator may not be zero. Normalization GCD) of n and d is 1 (use Euclid's algorithm-you can look this up); and n/d, where n is the numerator and d is the denominator. However, if the denominator is 1, then only the numerator nis printed. The fraction is always kept in the lowest terms, that is, the Greatest Common Divisor The denominator is never negative. Addition a/bc/d is (ad bc)/bd Subtraction a/b -c/d is (ad - bc)/bd Multiplication! (a/b) (c/d) is (a*c)/(b*d) * Division (/b / (c/d) is (a*d)/(b*c) Absolute Assuming that a/b is normalized: Valuea ?a b :-a / b Negation-(a/b) is -a/b Special Inverse of a/b is b/a Equality lowest terms, numerators are equal and denominators are equal. Comparison a/b is less than c/d if adbc Zero Zero is represented with a numerator of zero and a denominator of one. 1. Implement a calculator in C++ that works with fractions. You will need one class: Fraction - An object of this class represents a fraction. The class contains function for operating on the fraction. . Arithmetic with Fractions Components Two integers, known as the numerator and the denominator. How printed Restrictions The denominator may not be zero. Normalization GCD) of n and d is 1 (use Euclid's algorithm-you can look this up); and n/d, where n is the numerator and d is the denominator. However, if the denominator is 1, then only the numerator nis printed. The fraction is always kept in the lowest terms, that is, the Greatest Common Divisor The denominator is never negative. Addition a/bc/d is (ad bc)/bd Subtraction a/b -c/d is (ad - bc)/bd Multiplication! (a/b) (c/d) is (a*c)/(b*d) * Division (/b / (c/d) is (a*d)/(b*c) Absolute Assuming that a/b is normalized: Valuea ?a b :-a / b Negation-(a/b) is -a/b Special Inverse of a/b is b/a Equality lowest terms, numerators are equal and denominators are equal. Comparison a/b is less than c/d if adbc Zero Zero is represented with a numerator of zero and a denominator of one