C++ Programming: Matrix operations

skeleton code with function descriptions:

#ifndef MATRIX_TYPE #define MATRIX_TYPE #include using std::string; #include using std::vector; /* very convenient. If you want to change the type stored in the matrix, you only have to change the single template type in matrix_row */ using matrix_row = vector; using matrix = vector; /* nicely print a matrix. Should have row/column alignment converts it to a string (doesn't print to cout!!!) uses width to space elements (setw). Default is 3 */ string matrix_to_str(const matrix &m1, size_t width=3); /* true if the two matrices have the same shape false otherwise */ bool same_size(matrix &m1, matrix &m2); /* matrices must not be empty and must be the same shape: - if true, return a new matrix that adds m1+m2 - if false, return an empty matrix (no elements) */ matrix add(matrix &m1, matrix &m2); /* matrix must not be empty: - if true, multiply T scalar value by m - if false, return empty matrix (no elements) */ matrix scalar_multiply(matrix &m, long val); #endif 

A sample test for the code would look something like this:

#include #include matrix m1 ={ {0,1}, {1,2} }; matrix m2 ={ {1,1}, {1,1} }; matrix m = add(m1,m2); 

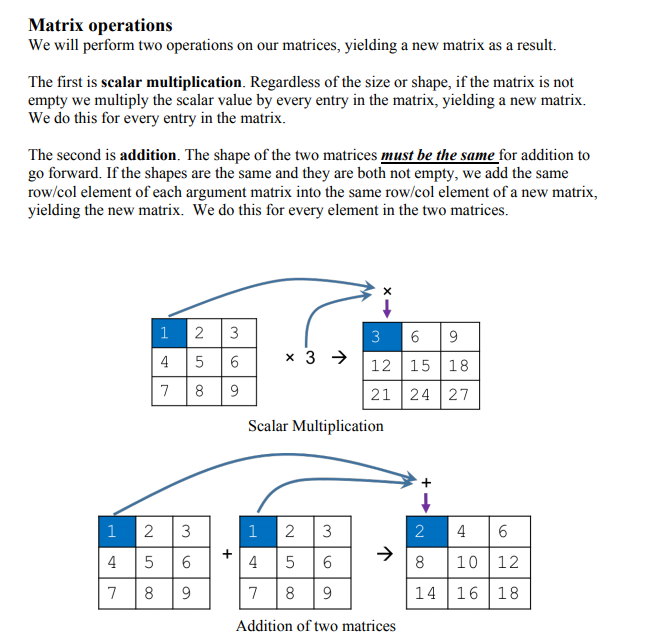
Matrix operations We will perform two operations on our matrices, yielding a new matrix as a result. The first is scalar multiplication. Regardless of the size or shape, if the matrix is not empty we multiply the scalar value by every entry in the matrix, yielding a new matrix. We do this for every entry in the matrix. The second is addition. The shape of the two matrices must be the same for addition to go forward. If the shapes are the same and they are both not empty, we add the same row/col element of each argument matrix into the same row/col element of a new matrix, yielding the new matrix. We do this for every element in the two matrices. 3 |12|15 | 18 21 24 27 4 5 6 Scalar Multiplication 2 7 8 9 14 16 18 Addition of two matrices Matrix operations We will perform two operations on our matrices, yielding a new matrix as a result. The first is scalar multiplication. Regardless of the size or shape, if the matrix is not empty we multiply the scalar value by every entry in the matrix, yielding a new matrix. We do this for every entry in the matrix. The second is addition. The shape of the two matrices must be the same for addition to go forward. If the shapes are the same and they are both not empty, we add the same row/col element of each argument matrix into the same row/col element of a new matrix, yielding the new matrix. We do this for every element in the two matrices. 3 |12|15 | 18 21 24 27 4 5 6 Scalar Multiplication 2 7 8 9 14 16 18 Addition of two matrices