C Program.Thanks!

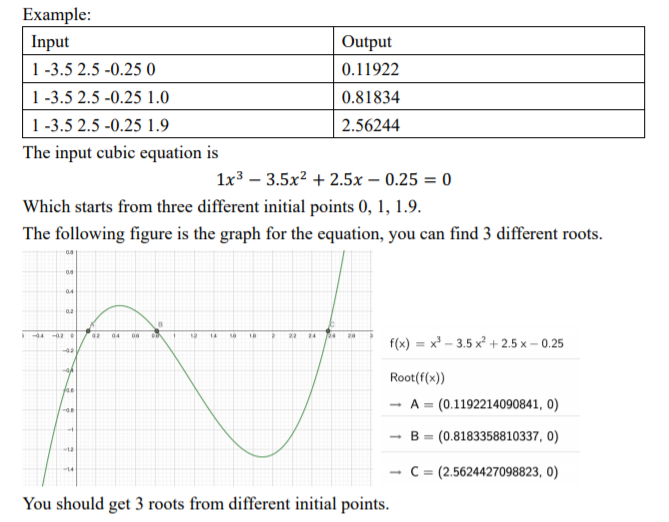
Problem 7: Cubic Equation Root (20%) In calculus, you should have learned to use Newton's Method to find the root of a function. Newton's Method is an approximation to guess the root from an initial point Xo. The process is repeated as f(xn) Xn+1 = xn f'(xn) where f' is the derivative of function f. A cubic function is an equation that can be written in general form f(x) = ax3 + bx2 + cx + d = 0 In this problem, you need to use C to implement a program that approximate a user input cubic equation from an initial point by Newton's Method. Given a,b,c,d and initial point Xo, print the approximated root of the equation. Note: Please print to five decimal places for the output(WE FIL). Example: Input Output 1 -3.5 2.5 -0.25 0 0.11922 1 -3.5 2.5 -0.25 1.0 0.81834 1-3.5 2.5 -0.25 1.9 2.56244 The input cubic equation is 1x3 3.5x2 + 2.5x - 0.25 = 0 Which starts from three different initial points 0, 1, 1.9. The following figure is the graph for the equation, you can find 3 different roots. 00 02 -02 04 1 14 2 22 94 f(x) = xl 3.5 x +2.5x -0.25 - - 100 Root(f(x)) A = (0.1192214090841, 0) - B = (0.8183358810337, 0) C = (2.5624427098823, 0) You should get 3 roots from different initial points