(c) Repeat part (b) above for c = 0.2

(d) What do you observe?

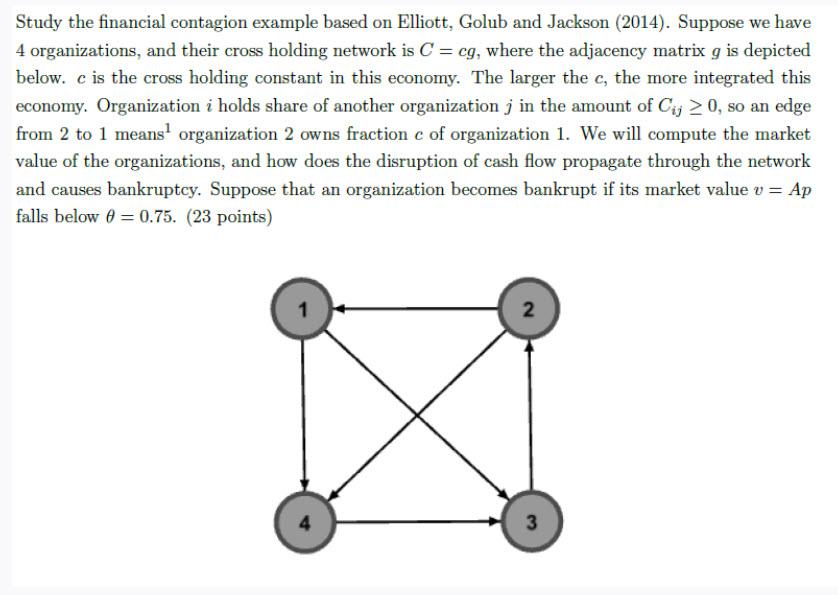
Study the financial contagion example based on Elliott, Golub and Jackson (2014). Suppose we have 4 organizations, and their cross holding network is C = cg, where the adjacency matrix g is depicted below. c is the cross holding constant in this economy. The larger the c, the more integrated this economy. Organization i holds share of another organization j in the amount of Cij > 0, so an edge from 2 to 1 means organization 2 owns fraction c of organization 1. We will compute the market 1 value of the organizations, and how does the disruption of cash flow propagate through the network and causes bankruptcy. Suppose that an organization becomes bankrupt if its market value v = Ap falls below 6 = 0.75. (23 points) 2 4 3 (a) Write out the adjacency matrix g. (1 points) (b) For c = 0.1 (10 points) i. Write out the matrix C = cg. (1 points) ii. Let u = 1-2; Cji be the fraction of organization i privately held. Write out the matrix . (3 points) ii. Compute A = (I C)-1. Write out A (Round to 2 decimal points). (Hint: You can compute the inverse of a matrix using the "solve function in R.) (2 points) iv. Suppose that a disruption of cash flow happens to one organization in the network (ie. its cash flow drops to 0), while the cash flow of the other organizations remain at 1. Which organizations become bankrupt, if this disruption happens to each organization in turn? Fill in the table below. (4 points) c= 0.1 Organizations that fail Cash flow of 1 gets disrupted Cash flow of 2 gets disrupted Cash flow of 3 gets disrupted Cash flow of 4 gets disrupted Study the financial contagion example based on Elliott, Golub and Jackson (2014). Suppose we have 4 organizations, and their cross holding network is C = cg, where the adjacency matrix g is depicted below. c is the cross holding constant in this economy. The larger the c, the more integrated this economy. Organization i holds share of another organization j in the amount of Cij > 0, so an edge from 2 to 1 means organization 2 owns fraction c of organization 1. We will compute the market 1 value of the organizations, and how does the disruption of cash flow propagate through the network and causes bankruptcy. Suppose that an organization becomes bankrupt if its market value v = Ap falls below 6 = 0.75. (23 points) 2 4 3 (a) Write out the adjacency matrix g. (1 points) (b) For c = 0.1 (10 points) i. Write out the matrix C = cg. (1 points) ii. Let u = 1-2; Cji be the fraction of organization i privately held. Write out the matrix . (3 points) ii. Compute A = (I C)-1. Write out A (Round to 2 decimal points). (Hint: You can compute the inverse of a matrix using the "solve function in R.) (2 points) iv. Suppose that a disruption of cash flow happens to one organization in the network (ie. its cash flow drops to 0), while the cash flow of the other organizations remain at 1. Which organizations become bankrupt, if this disruption happens to each organization in turn? Fill in the table below. (4 points) c= 0.1 Organizations that fail Cash flow of 1 gets disrupted Cash flow of 2 gets disrupted Cash flow of 3 gets disrupted Cash flow of 4 gets disrupted