Cal 2

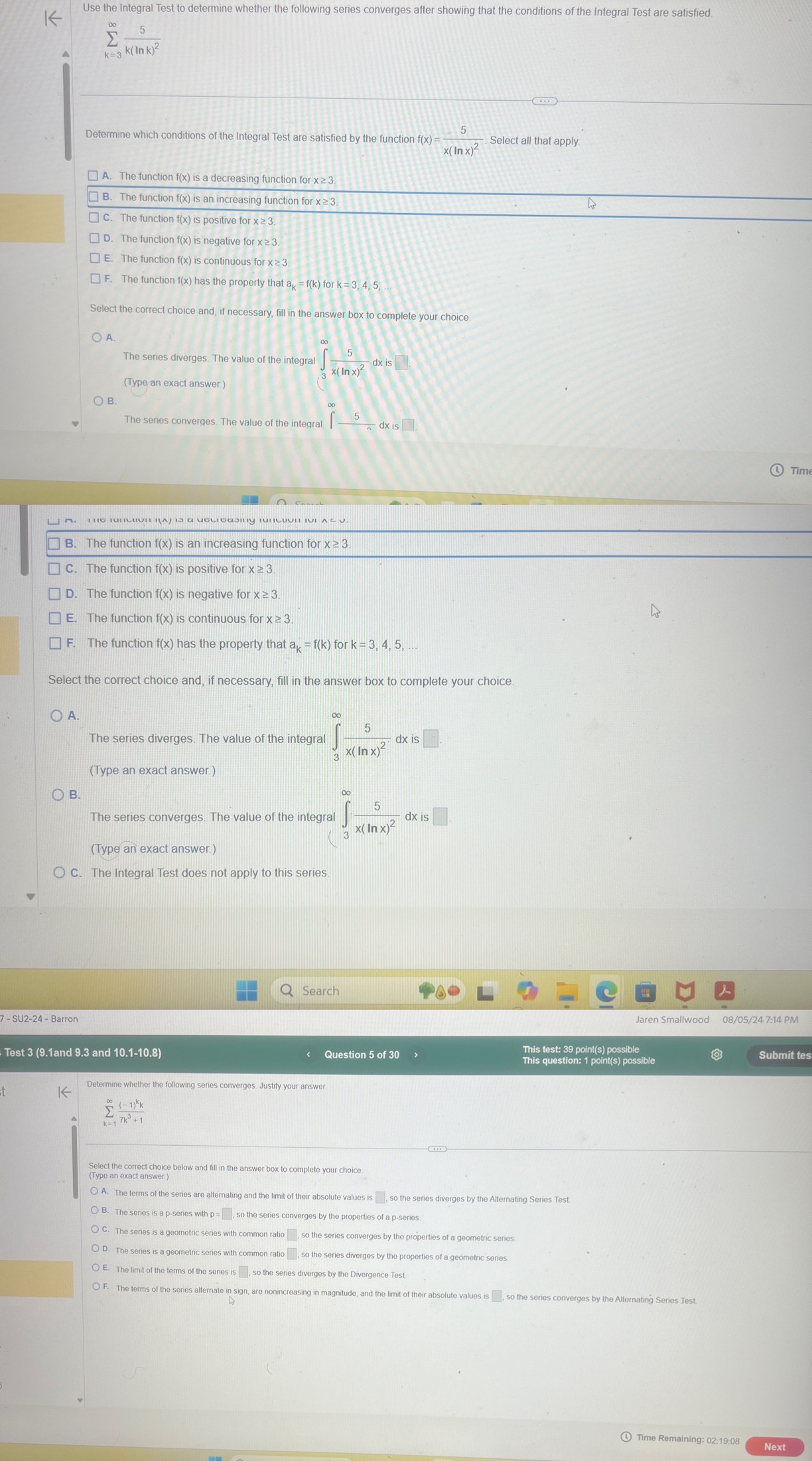
K Use the Integral Test to determine whether the following series converges after showing that the conditions of the Integral Test are satisfied. 00 5 k=3 K( In k) 2 5 Determine which conditions of the Integral Test are satisfied by the function f(X) Select all that apply. x( In x)2 A. The function f(x) is a decreasing function for x 2 3. B. The function f(x) is an increasing function for x 2 3 c. The function f(x) is positive for x 2 3. D. The function f(x) is negative for x 2 3. [E. The function f(x) is continuous for x 2 3. [F. The function f(x) has the property that ax = f(k) for k = 3, 4, 5, Select the correct choice and, if necessary, fill in the answer box to complete your choice. O A. 00 The series diverges. The value of the integral 5 X( In x)2 0 dx is (Type an exact answer.) B. The series converges. The value of the integral 5 dx is Tim B. The function f(x) is an increasing function for x = 3 C. The function f(x) is positive for x 2 3. D. The function f(x) is negative for x = 3. E. The function f(x) is continuous for x 2 3. F. The function f(x) has the property that a, = f(k) for k - 3, 4, 5, ... Select the correct choice and, if necessary, fill in the answer box to complete your choice. OA. 5 The series diverges. The value of the integral dx is 3 X( In x) (Type an exact answer.) O B. 5 The series converges. The value of the integral dx is X( In x)2 (Type an exact answer.) O C. The Integral Test does not apply to this series. Q Search - SU2-24 - Barron Jaren Smallwood 08/05/24 7:14 PM Test 3 (9.1and 9.3 and 10.1-10.8) Question 5 of 30 This test: 39 point(s) possible This question: 1 point(s) possible Submit te K Determine whether the following series converges, Justify your answer. 5 ( 1)K K=1 7k + 1 Select the correct choice below and fill in answer box to complete your choice. (Type an exact answer) A. The terms of the series are alternating and the limit of their absolute values is , so the series diverges by the Alternating Series Test. O B. The series is a p-series with p= . so the series converges by the properties of a p-series. O C. The series is a geometric series with common ratio , so the series converges by the properties of a geometric series. O D. The series is a geom ries with common ratio , so the series diverges by the properties of a geometric series. O E. The limit of the terms of the series is . so the series diverges by the Divergence Test. OF. The terms of the series alternate in sign, are nonincreasing in magnitude, and the limit of their absolute values is , so the series converges by the Alternating Series Test. Time Remaining: 02:19:08 Next