Calculate all

The two random variables in Exercise 11.6 are special cases of

Gam(?, ?) variables, namely with ? = 2 and ? = 1/2. More generally, let11.5 Exercises 165

X1,...,Xn be independent Gam(k, ?) distributed random variables, where

? > 0 and k is a positive integer. Argue?without doing any calculations?

that X1 + + Xn has a Gam(nk, ?) distribution.

11.8 We investigate the effect on the Cauchy distribution under a change of

units.

a. Let X have a standard Cauchy distribution. What is the distribution of

Y = rX + s?

b. Let X have a Cau(?, ?) distribution. What is the distribution of the

random variable (X ? ?)/??

11.9 Let X and Y be independent random variables with a Par (?) and

Par (?) distribution.

a. Take ? = 3 and ? = 1 and determine the probability density of Z = XY .

b. Determine the probability density of Z = XY for general ? and ?.

11.10 Let X and Y be independent random variables with a Par (?) and

Par (?) distribution.

How many ways are there to permute the letters in the word MISSISSIPPI?

2. (a) How many 7-digit phone numbers are possible, assuming that the first digit can't

be a 0 or a 1?

(b) Re-solve (a), except now assume also that the phone number is not allowed to start

with 911 (since this is reserved for emergency use, and it would not be desirable for the

system to wait to see whether more digits were going to be dialed after someone has

dialed 911).

3. Fred is planning to go out to dinner each night of a certain week, Monday through

Friday, with each dinner being at one of his ten favorite restaurants.

(a) How many possibilities are there for Fred's schedule of dinners for that Monday

through Friday, if Fred is not willing to eat at the same restaurant more than once?

(b) How many possibilities are there for Fred's schedule of dinners for that Monday

through Friday, if Fred is willing to eat at the same restaurant more than once, but is

not willing to eat at the same place twice in a row (or more)?

4. A round-robin tournament is being held with n tennis players; this means that every

player will play against every other player exactly once.

(a) How many possible outcomes are there for the tournament (the outcome lists out

who won and who lost for each game)?

(b) How many games are played in total?

5. A knock-out tournament is being held with 2n tennis players. This means that for each

round, the winners move on to the next round and the losers are eliminated, until only

one person remains. For example, if initially there are 24 = 16 players, then there are

8 games in the first round, then the 8 winners move on to round 2, then the 4 winners

move on to round 3, then the 2 winners move on to round 4, the winner of which is

declared the winner of the tournament. (There are various systems for determining who

plays whom within a round, but these do not matter for this problem.)

(a) How many rounds are there?

(b) Count how many games in total are played, by adding up the numbers of games

played in each round.

(c) Count how many games in total are played, this time by directly thinking about it

without doing almost any calculation.

Hint: How many players need to be eliminated?

6. There are 20 people at a chess club on a certain day. They each find opponents and

start playing. How many possibilities are there for how they are matched up, assuming

that in each game it does matter who has the white pieces (in a chess game, one player

has the white pieces and the other player has the black pieces)

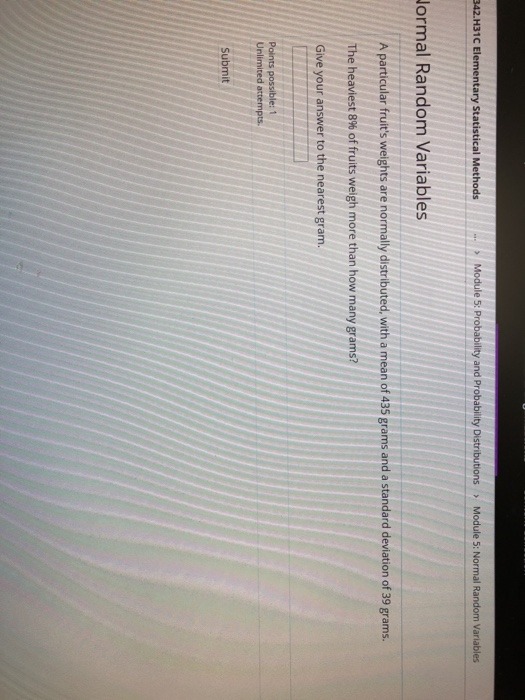
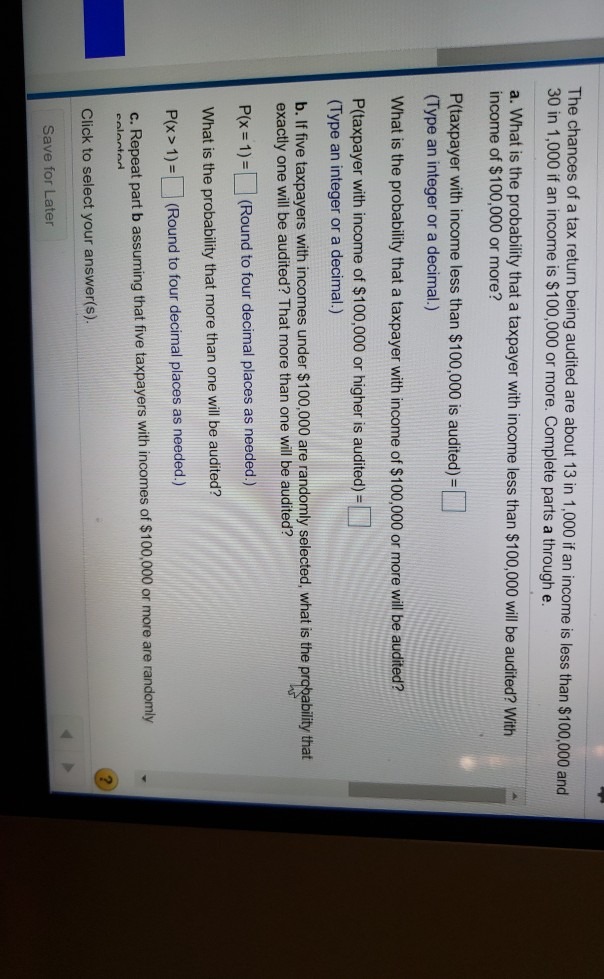
342.H31C Elementary Statistical Methods Module 5: Probability and Probability Distributions > Module 5: Normal Random Variables ormal Random Variables A particular fruit's weights are normally distributed, with a mean of 435 grams and a standard deviation of 39 grams. The heaviest 89% of fruits weigh more than how many grams? Give your answer to the nearest gram. Points possible: 1 Unlimited attempts. SubmitDuring 2010, the United States performed its every-ten-year census. Suppose that the Census Bureau sampled (names generated by the computer, with replacement) 1000 residents of Massachusetts (population: 6,000,000) and asked them to fill out a more detailed census form. Let X = the number of people in this sample who live in the greater Boston (Massachusetts) area (population: 2,000,000). Then (circle your answer and explain your choice); (a) X is a binomial random variable with n = 6, 000, 000 and 0 = =. (b ) X is not a binomial random variable since the events "Massachusetts resident" and "greater Boston resident" are not independent. (c) X is a binomial random variable with n = 1000 and 8 = 2. (d) X is not a binomial random variable because there are more than two outcomes with respect to where a person might live. (e) X is a binomial random variable with n = 1000 and d = 6000The chances of a tax return being audited are about 13 in 1,000 if an income is less than $100,000 and 30 in 1,000 if an income is $100,000 or more. Complete parts a through e. a. What is the probability that a taxpayer with income less than $100,000 will be audited? With income of $100,000 or more? P(taxpayer with income less than $100,000 is audited) = (Type an integer or a decimal.) What is the probability that a taxpayer with income of $100,000 or more will be audited? P(taxpayer with income of $100,000 or higher is audited) = (Type an integer or a decimal.) b. If five taxpayers with incomes under $100,000 are randomly selected, what is the probability that 4 exactly one will be audited? That more than one will be audited? P(x =1) =|(Round to four decimal places as needed.) What is the probability that more than one will be audited? P(x > 1) = (Round to four decimal places as needed.) c. Repeat part b assuming that five taxpayers with incomes of $100,000 or more are randomly eplanted Click to select your answer(s). Save for Later