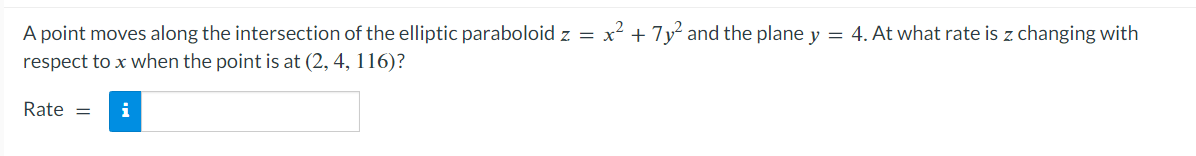
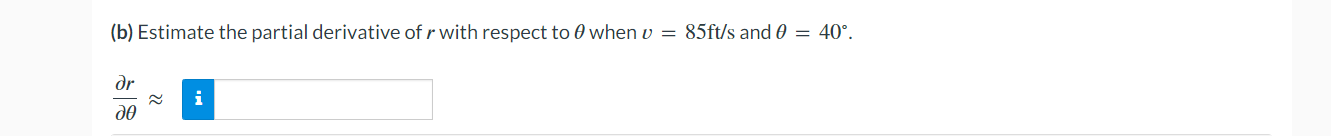
Calculus 1

Content Covered:

- Rectangular Coordinates in 3-Space; Spheres; Cylindrical Surfaces

- Quadric Surfaces

- Partial Derivatives

- The Chain Rule

- Maxima and Minima of Functions of Two Variables

Directions:Kindly answer each of the following problems below. And also, please indicate the complete solution. I promise that I will give you a good rating after this. Thank you so much for helping me out.

11)

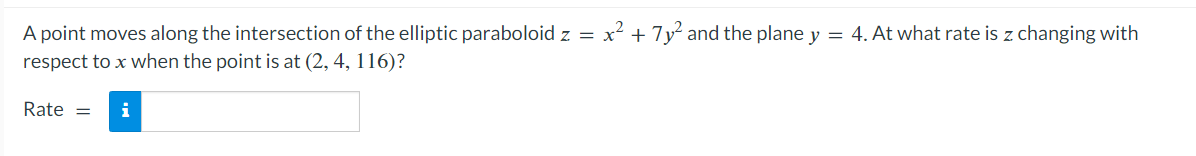
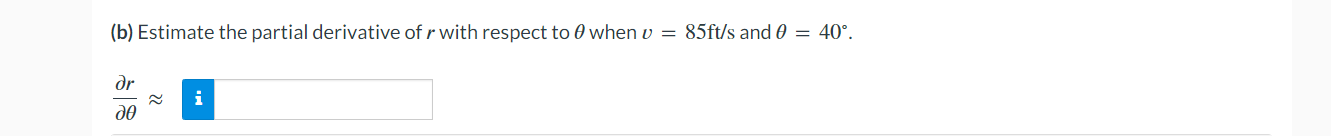
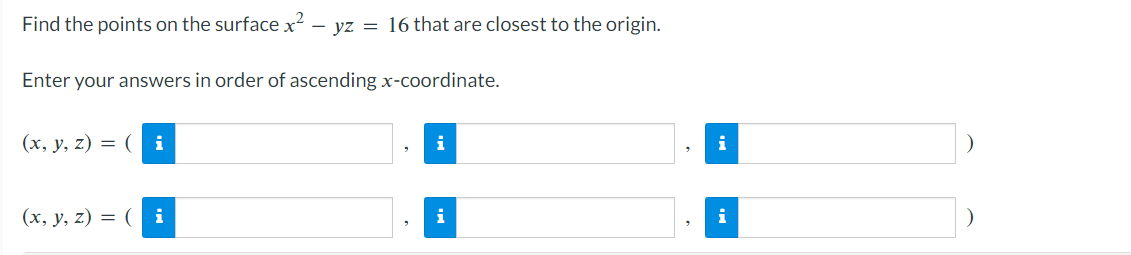
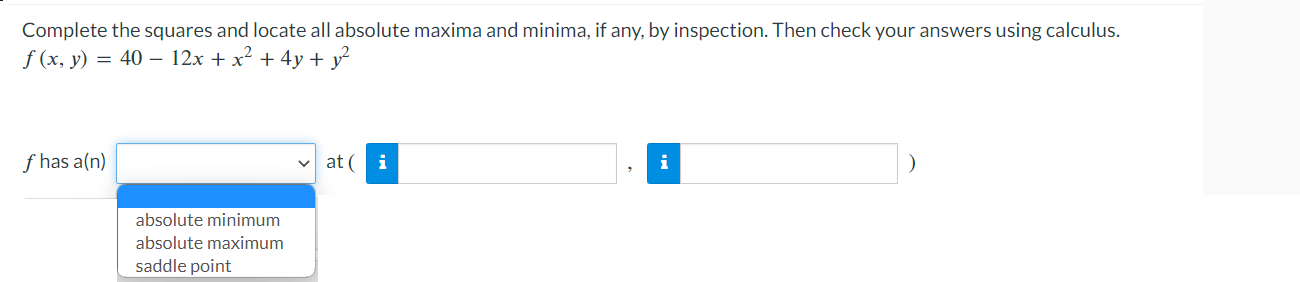
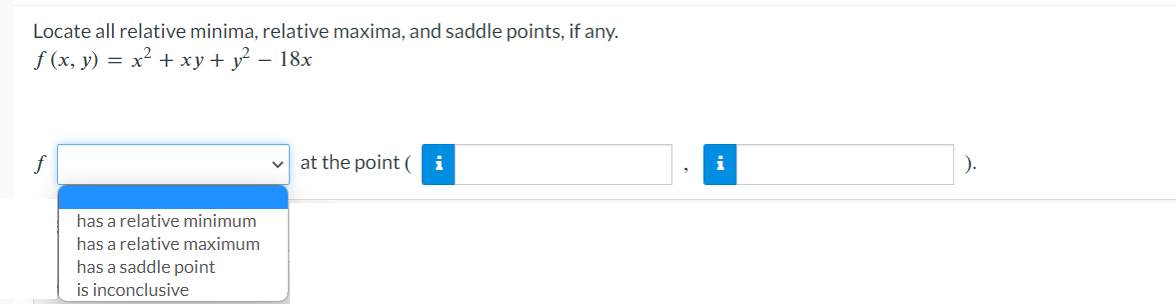
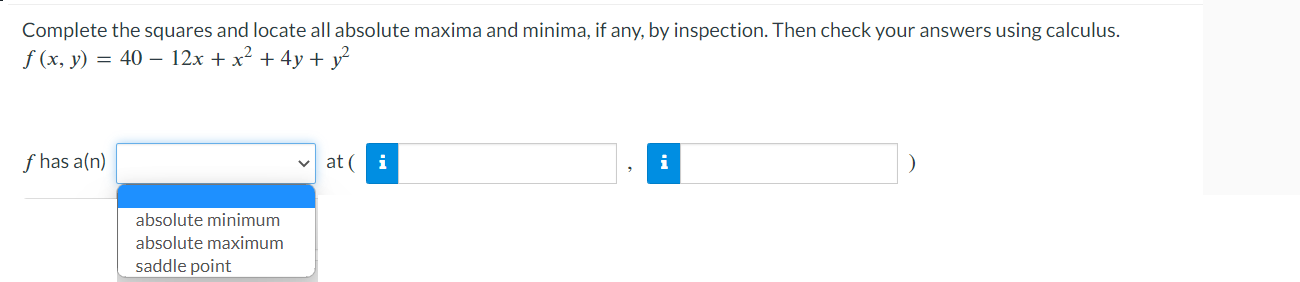
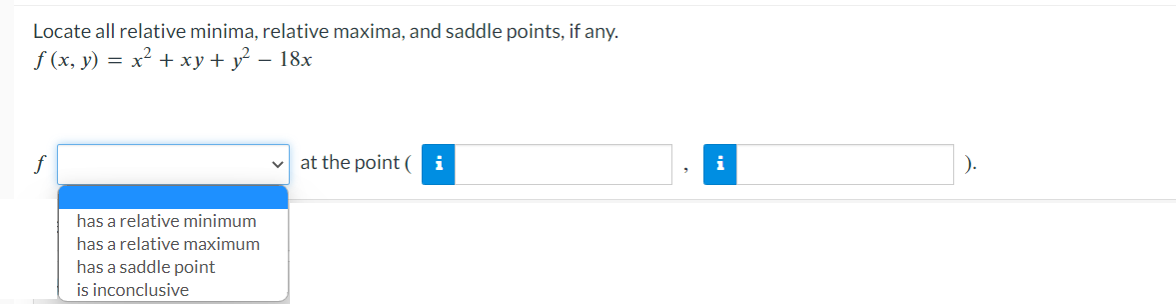
\fConfirm that the mixed second-order partial derivatives of f are the same. f(x, y) = el sin(y) fxy fyx =A point moves along the intersection of the elliptic paraboloid z : x2 + 7y2 and the plane y : 4. At what rate is z changing with respect to x when the point is at (2, 4. 116)? Rate : n (b) Estimate the partial derivative of r with respect to 0 when u = 85ft/s and 0 = 40. or ~ iSuppose that Nolan throws a baseball to Ryan and that the baseball leaves Nolan's hand at the same height at which it is caught by Ryan. If we ignore air resistance, the horizontal range r of the baseball is a function of the initial speed v of the ball when it leaves Nolan's hand and the angle 0 above the horizontal at which it is thrown. SPEED v (ft/s) 75 80 85 90 35 165 188 212 238 40 173 197 222 249 ANGLE O (degrees) 45 176 200 226 253 50 173 197 222 249 Use the accompanying table and the equations below to estimate the partial derivatives. fx (xo, yo) = lim f (xo + Ax, yo) - f (xo, yo) ; fy (xo, yo) = lim f (xo, yo + Ay) - f (xo, yo) 4x-0 Ax 4y-0 Ay Take a left-hand estimate and a right-hand estimate in each case and give the average of the two as your final answer. (a) Estimate the partial derivative of r with respect to v when v = 85ft/s and 0 = 40'. or ~2 Find the points on the surface 2: yz = 16 that are closest to the origin. Enter your answers in order of ascending x-coordinate. (x,y,z)=( (x,y,z)=( Complete the squares and locate all absolute maxima and minima, if any, by inspection. Then check your answers using calculus. f(x,y):4012x+x2+4y+y2 absolute minimum absolute maximum \\ saddle point awn ,n > (b) Find the maximum and minimum values of f on each diagonal of the square. Maximum Minimum y =x : f(x, y) = f ( x, y) = y = 1 -x: f(x, y) = f ( x, y ) = (c) Find the maximum and minimum values of f on the entire square. Maximum Minimum Entire square f(x, y) = f (x, y) =Consider the function f(x, y) = 8x2 - 5y + 4xy over the unit square 0