calculus 2

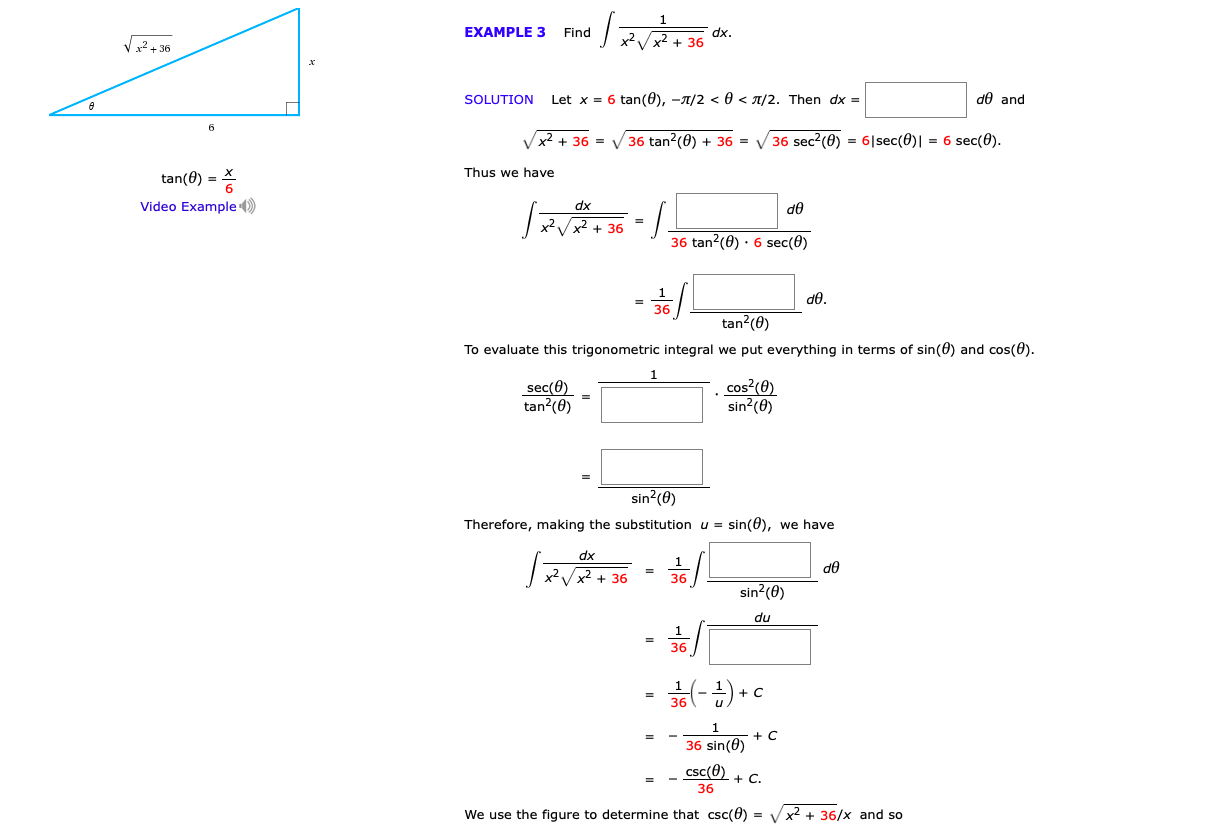
EXAMPLE 3 Find x2 Vx2 + 36 " dx. V x2+ 36 SOLUTION Let x = 6 tan(0), -71/2 /2. Then dx = do and 6 V x2 + 36 = \\ 36 tan2(0) + 36 = \\ 36 sec2(0) = 6|sec(0)| = 6 sec(0). tan(0) = x Thus we have Video Example () dx x2 V x2 + 36 36 tan (0) . 6 sec(0) 36 do. tanz(0) To evaluate this trigonometric integral we put everything in terms of sin(0) and cos(0). sec(0) - cos?(0) tan?(0) sin2(0) sin (0) Therefore, making the substitution u = sin(0), we have dx x2 Vx2 + 36 = 36 de sin-(0) du = 36 = 1 ( - 1 ) +C = - - 36 sin(0) -+ C CSC() + C. 36 We use the figure to determine that csc(0) = v x2 + 36/x and soWe use the figure to determine that csc(0) = v x2 + 36/x and so dx x2 + 36 + C