Question: Calculus 2: Section 7.2: Problem 12 (1 point) Find the volume formed by rotating the region enclosed by: y = 3vc and y = x




Calculus 2:



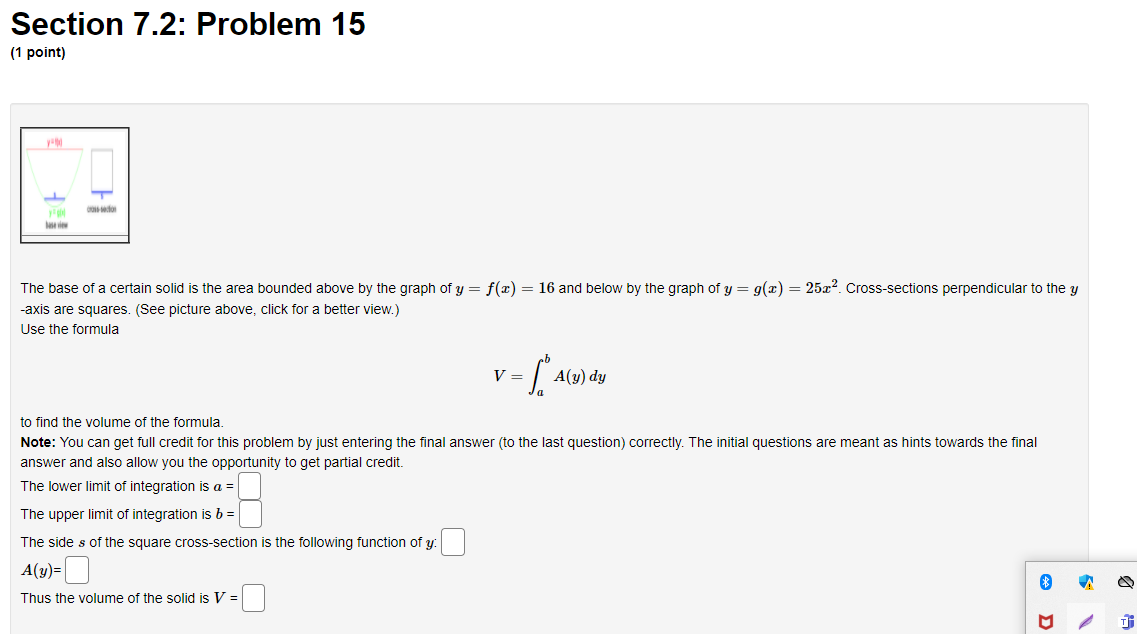
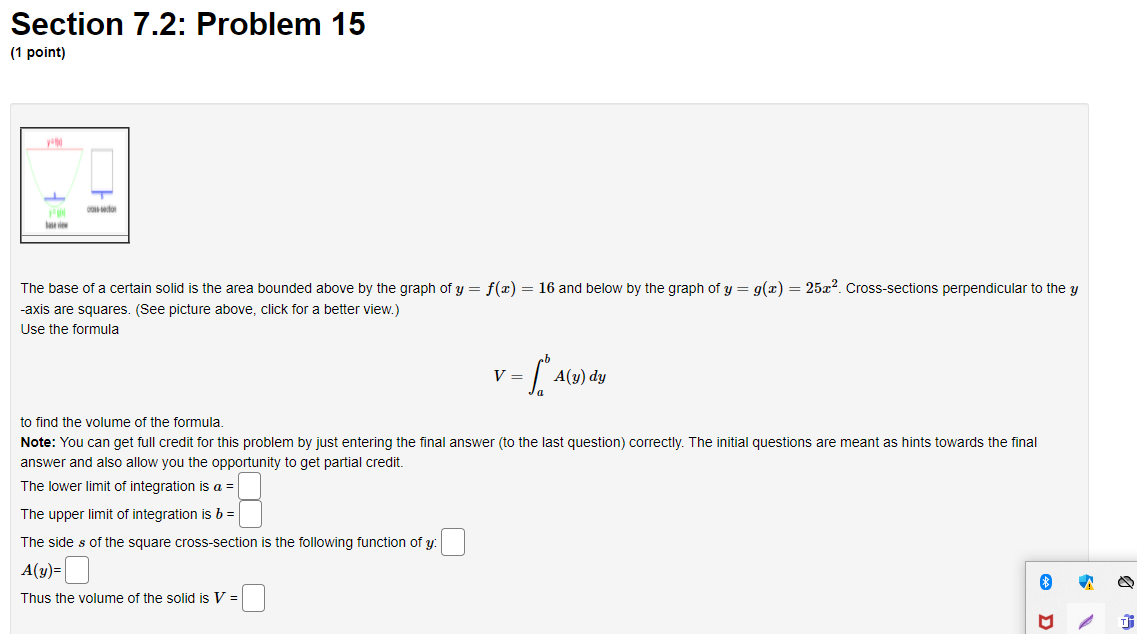
![z] = 16 and below by the graph of y = 9(2)](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6677762ce455f_0686677762cb177b.jpg)

Section 7.2: Problem 12 (1 point) Find the volume formed by rotating the region enclosed by: y = 3vc and y = x about the line y = 9Section 7.2: Problem 13 (1 point) Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. 1= J, y=0, 1 = 4, 1 = 5; about y = -1Section 7.2: Problem 14 (1 point) Find the volume formed by rotating the region enclosed by: y = 3vc and y = x about the line x = 10Section 7.2: Problem 15 (1 point) The base of a certain solid is the area bounded above by the graph of y = z] = 16 and below by the graph of y = 9(2) = 251-2. Crosssections perpendicular to the y axis are squares. (See picture above, click for a better View.) USE! the formula V=_/:A[y)dy to nd the volume of the formula. Note: You can get full credit forthis problem by just entering the nal answer (to the last question) conectly. The initial questions are meant as hints towards the nal answer and also allow you the opportunity to get partial credit. The lower limit of integration is a. = The upper limit of integration is b = The side a of the square crosssection is the following function of y: C] met] Or & Thus the volume of the solid is V = E] U I TI Section 7.2: Problem 16 (1 paint) The base of a solid is a circular disk with radius 6. Parallel cross sections perpendicular to the base are squares. Find the volume of the solid. D Section 7.2: Problem 17 (1 point) Find the volume of a frustum of a pyramid with square base of side 17, square top of side 7 and height 10. Volume=Section 7.2: Problem 18 (1 point) Find the volume of a frustum of a right circular cone with height 20, lower base radius 34 and top radius 19. Volume =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


