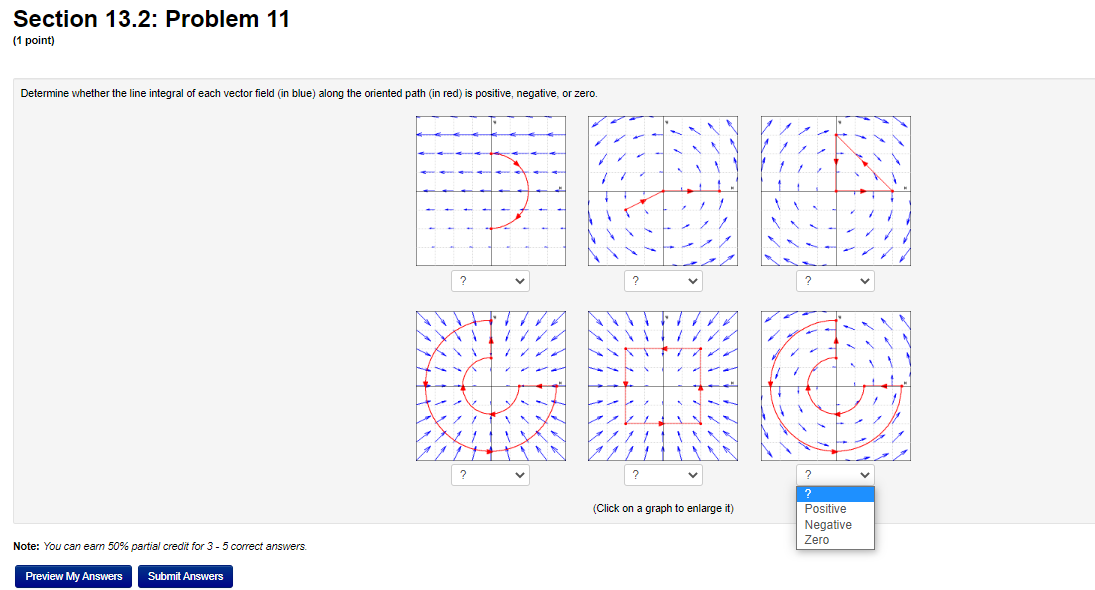
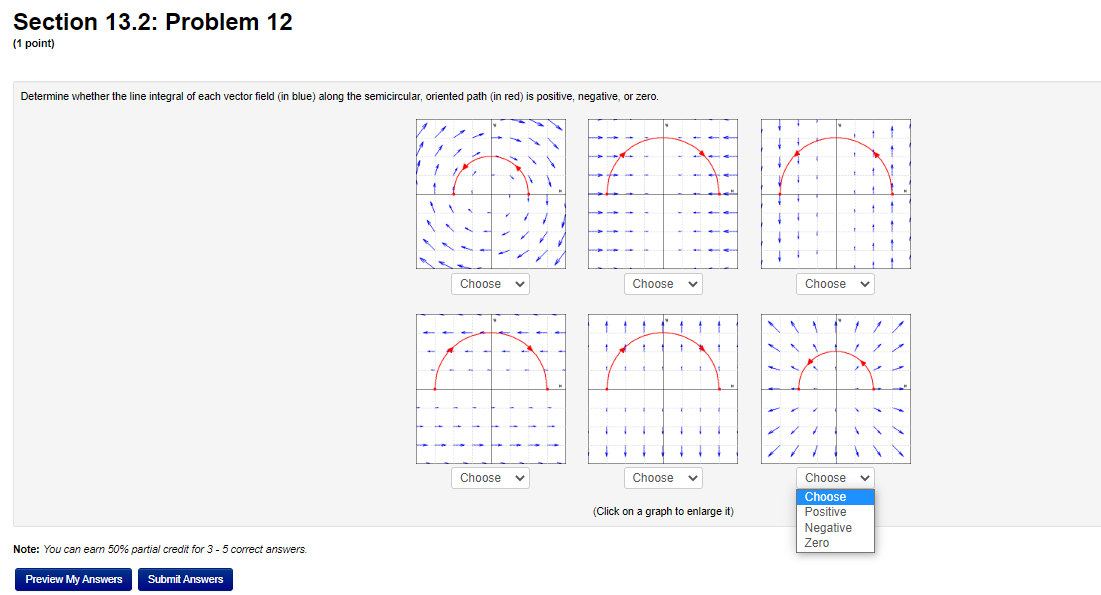
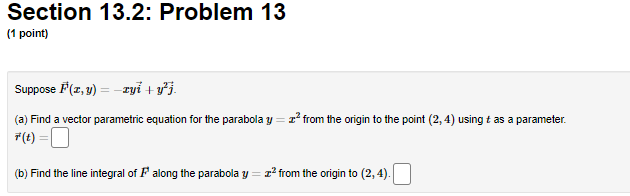
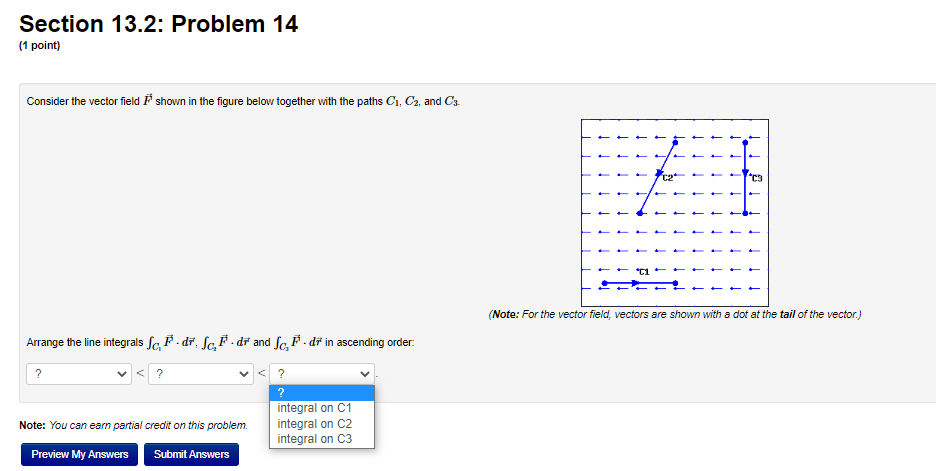
Calculus 3 :

final answer only, no explanation needed

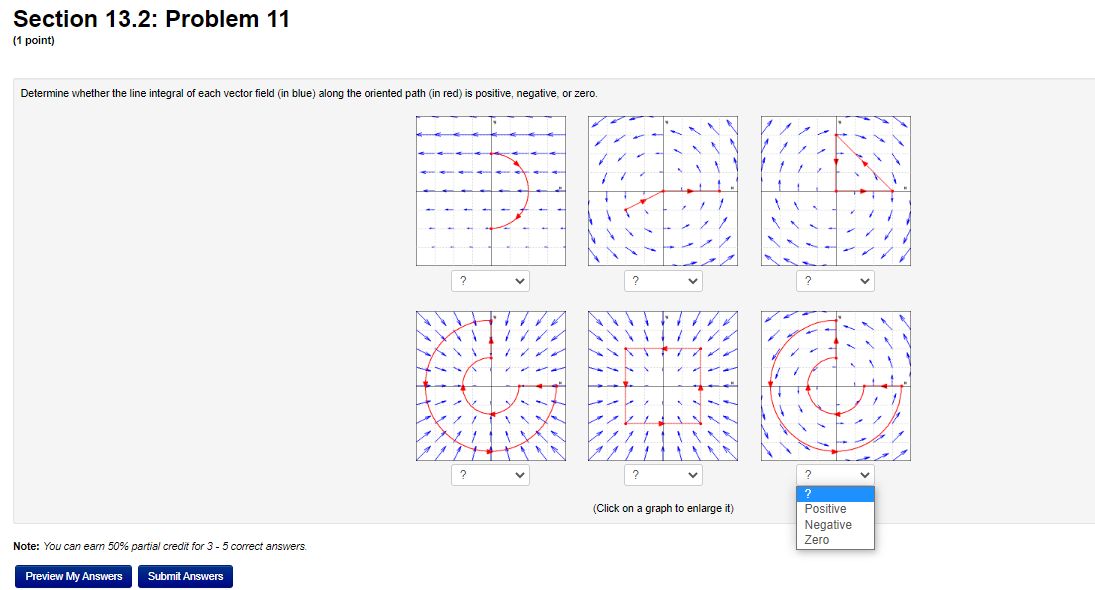
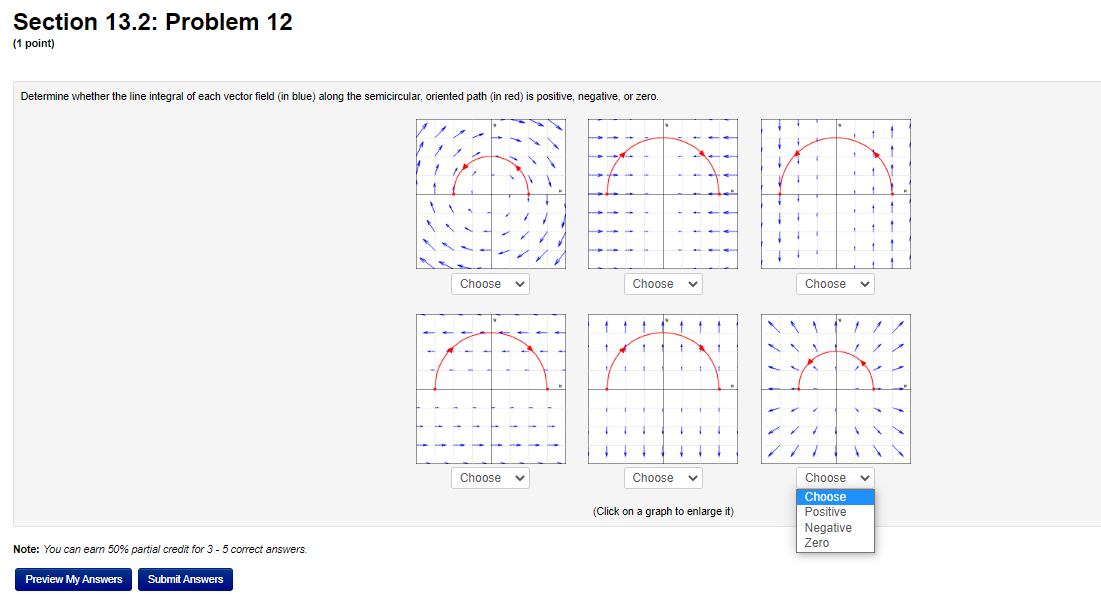
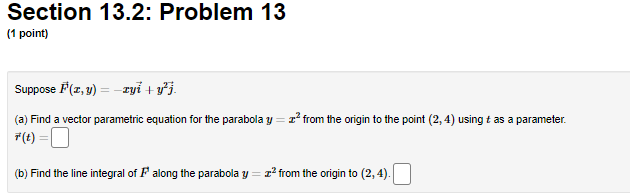
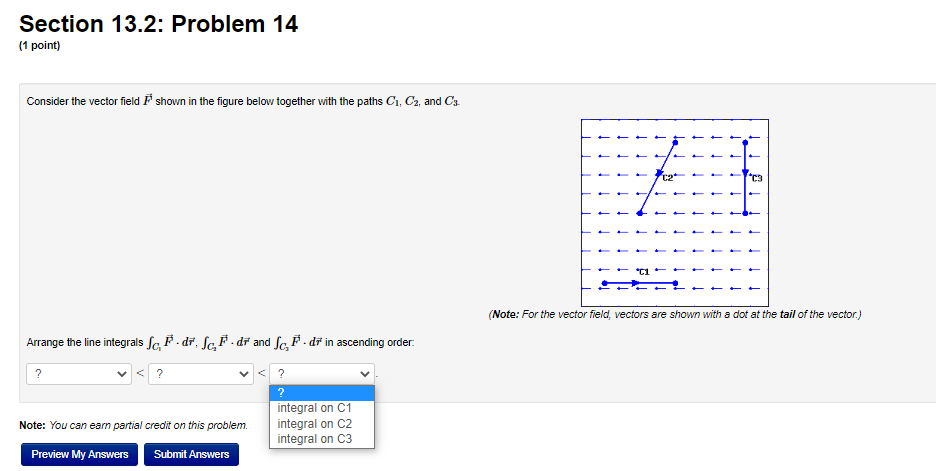
Section 13.2: Problem 8 (1 point) Find the work done by the force field F(I, V, 2) = cityj + 6k on a particle that moves along the helix r(#) = 6 cos(#) i + 6sin(t) j + 2tk, 0 0. Without computing them, determine for the following vector fields F whether the line integrals F . dr are positive, negative, or zero and type P, N, or Z as appropriate. A. F = the radial vector field = ri + wi: B. F = the circulating vector field = -vi + zj: C. F = the circulating vector field = yi - zj: D. F = the constant vector field = i + j:Section 13.2: Problem 10 (1 point) A curve C is given by a vector function r(t), 6