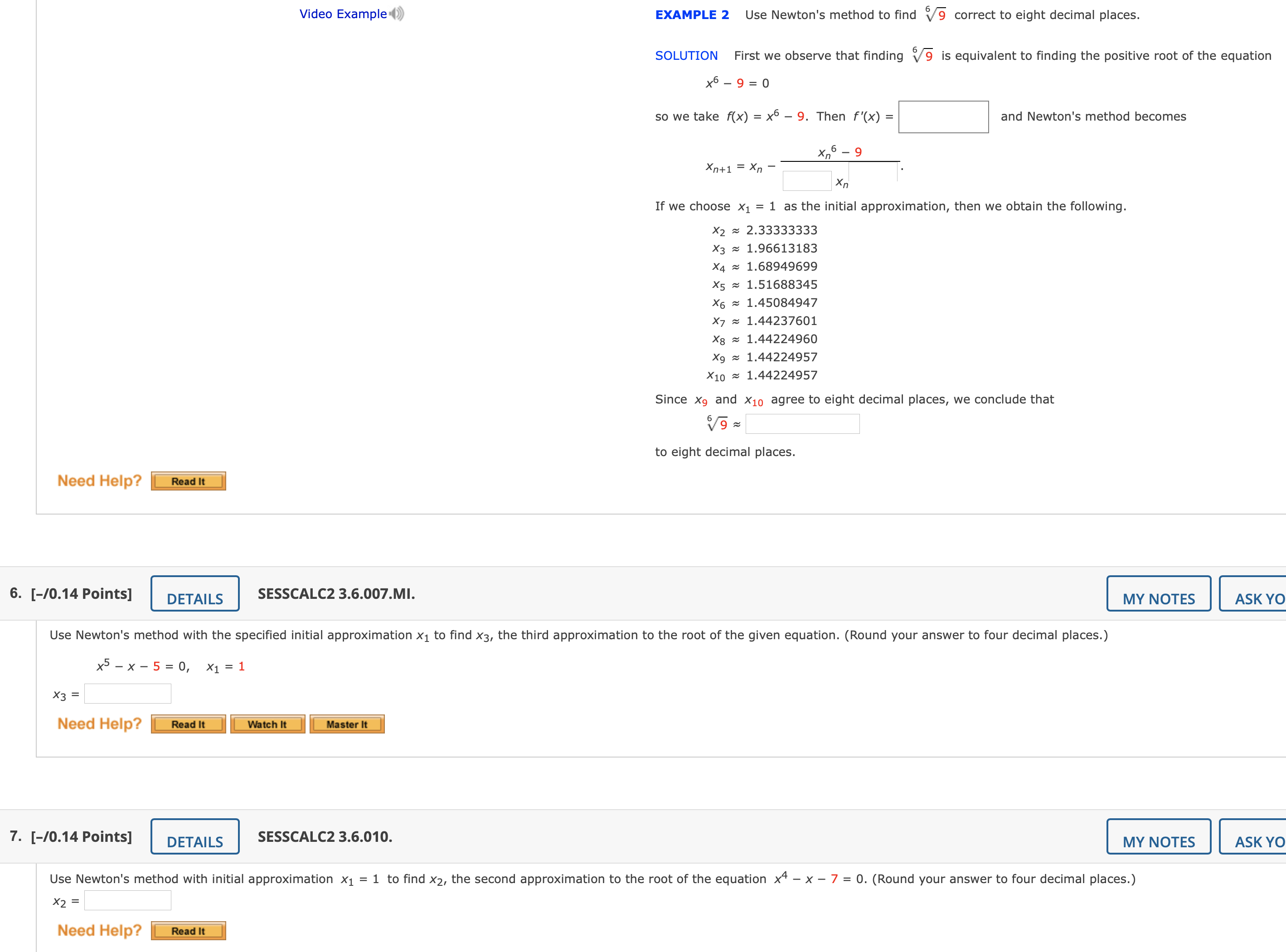
Question: Calculus: 5-7 Video Example () EXAMPLE 2 Use Newton's method to find 9 correct to eight decimal places. SOLUTION First we observe that finding

Calculus:
5-7
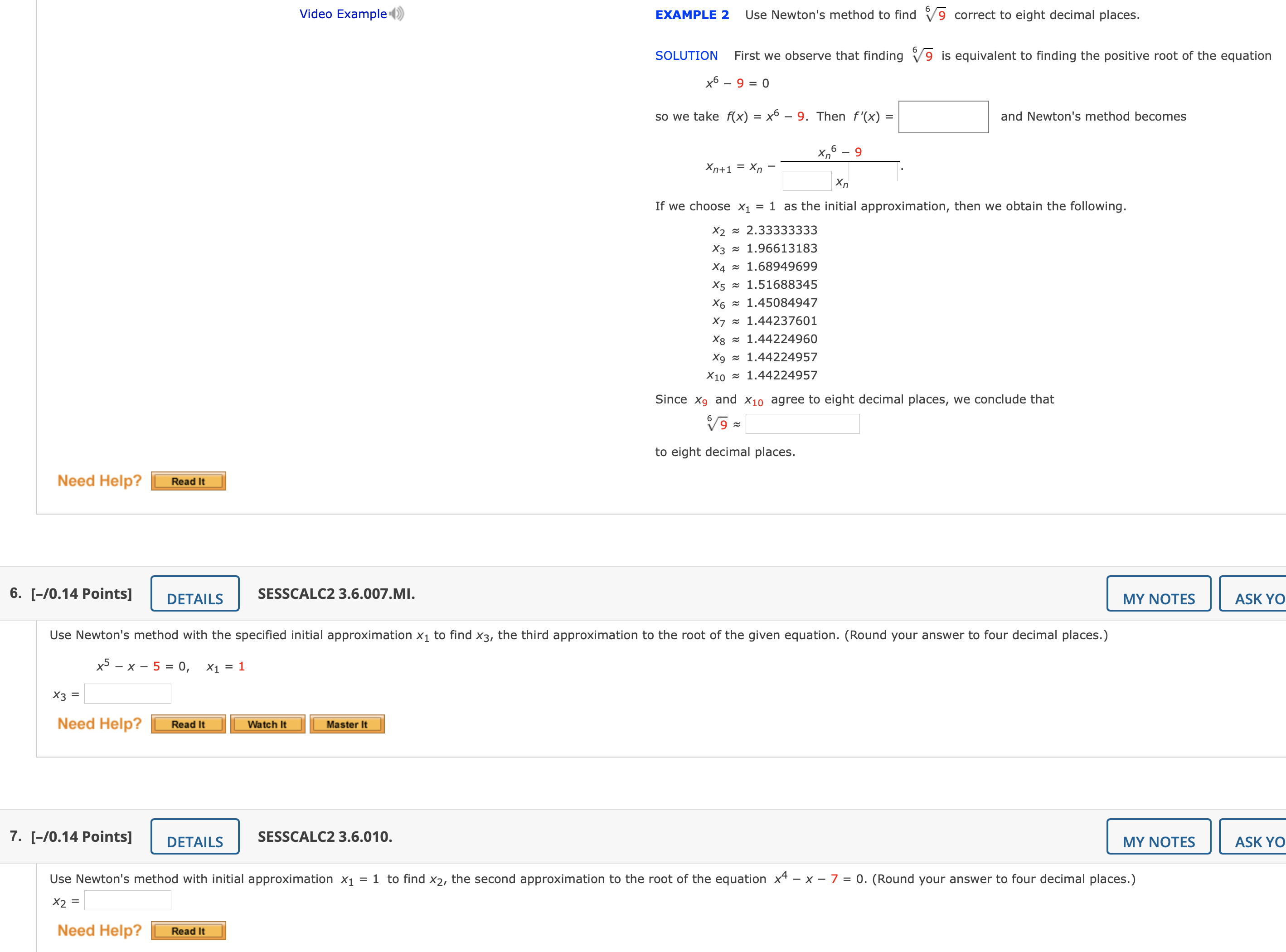

Video Example () EXAMPLE 2 Use Newton's method to find \\ 9 correct to eight decimal places. SOLUTION First we observe that finding V 9 is equivalent to finding the positive root of the equation x6 - 9 = 0 so we take f(x) = x6 - 9. Then f'(x) = and Newton's method becomes x 6 - 9 Xn+1 = Xn - Xn If we choose x1 = 1 as the initial approximation, then we obtain the following. X2 ~ 2.33333333 X3 ~ 1.96613183 X4 ~ 1.68949699 X5 = 1.51688345 X6 = 1.45084947 X7 ~ 1.44237601 X8 ~ 1.44224960 X9 ~ 1.44224957 X10 ~ 1.44224957 Since X9 and X10 agree to eight decimal places, we conclude that to eight decimal places. Need Help? Read It 6. [-/0.14 Points] DETAILS SESSCALC2 3.6.007.MI. MY NOTES ASK Y Use Newton's method with the specified initial approximation x1 to find x3, the third approximation to the root of the given equation. (Round your answer to four decimal places.) x5 - x - 5 = 0, X1 = 1 X3 = Need Help? Read It Watch It Master It 7. [-/0.14 Points] DETAILS SESSCALC2 3.6.010. MY NOTES ASK Y Use Newton's method with initial approximation x1 = 1 to find x2, the second approximation to the root of the equation x4 - x - 7 = 0. (Round your answer to four decimal places.) X2 = Need Help? Read ItLab 8: Extreme Values Part 1: Find the relative (local) and absolute (global) extreme values. 1. f (x) =x4+4x3 -8x2+5 a) Find the derivative. b) Find the critical numbers. Critical Numbers: X X = X = c) Use the First Derivative Test to determine if each Critical Numbers critical number is a relative maximum, relative A relative max minimum, or not a turning point at all. X = is: O A relative min Not a turning point at all O A relative max X= is: O A relative min O Not a turning point at all O A relative max X= is A relative min Not a turning point at all d) Find the absolute maximum on the interval [-1,1]. e) Find the absolute minimum on the interval [-1,1]. f) Find the absolute maximum on the interval [0,3]. g) Find the absolute minimum on the interval [0,3]
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


