Question: Calculus and vectors (LINEAR SYSTEMS) Please show all work leading to answer 1. Determine vector and parametric equations for the following lines that pass through
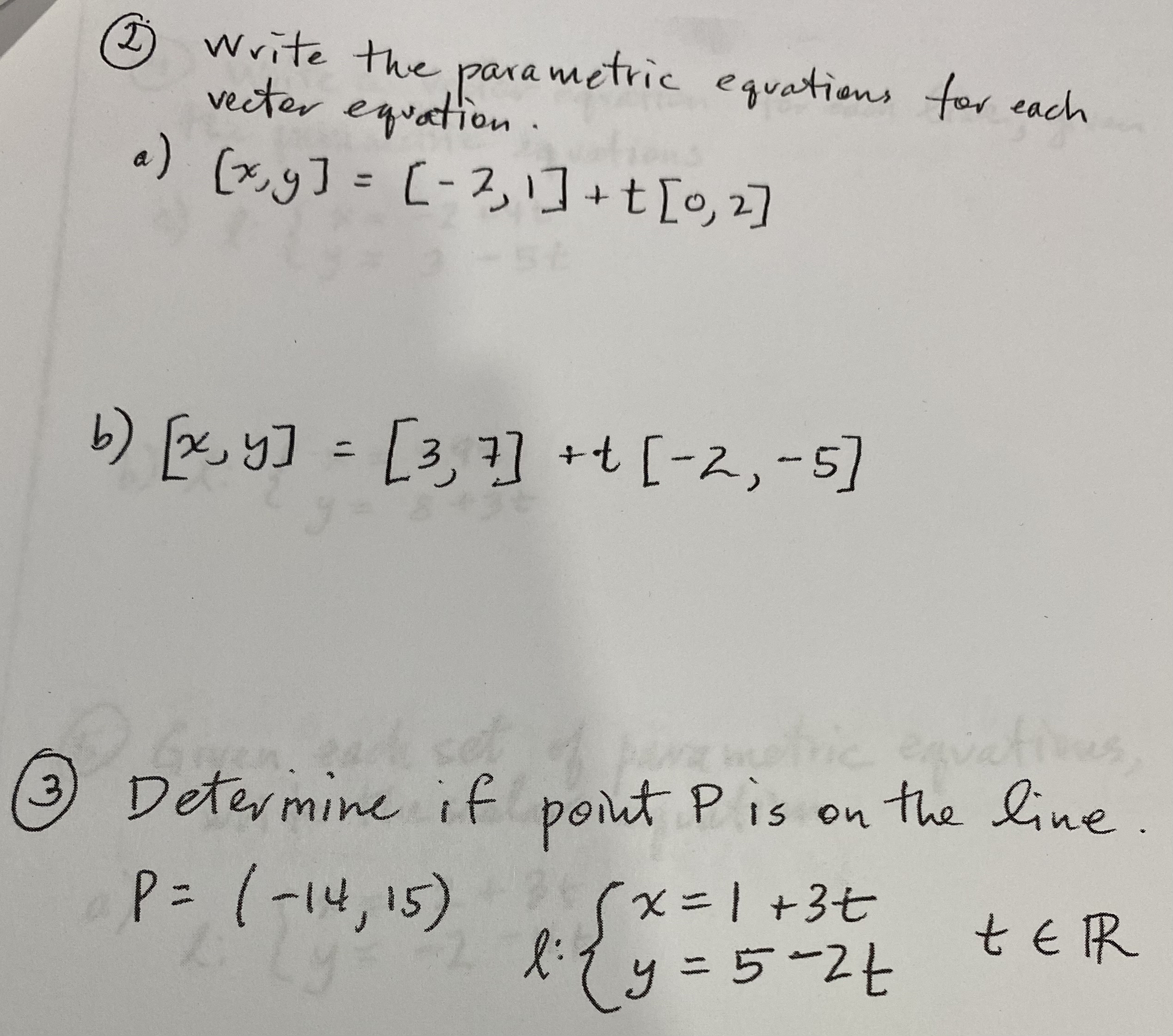


![equations for each vector equation a ) [ x , y ]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66652981a40da_79366652981807ed.jpg)
![= [ - 2 , 1] + t [0, 2] 6 )](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66652982150fe_79366652981e4217.jpg)
Calculus and vectors (LINEAR SYSTEMS)
Please show all work leading to answer
1. Determine vector and parametric equations for the following lines that pass through the points.
a) Q(0,7) , R(0,9) b) M(4,5) , N(9,5)
![[xx, y] = [3, 7] + + [- 2, -5] (3) Determine](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666529826fa27_794666529824d5e5.jpg)


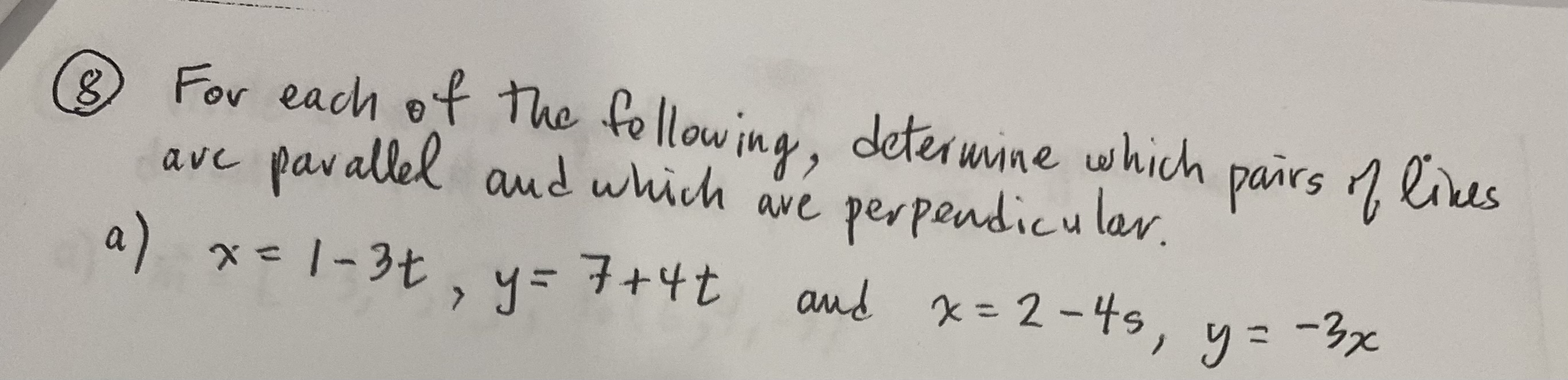
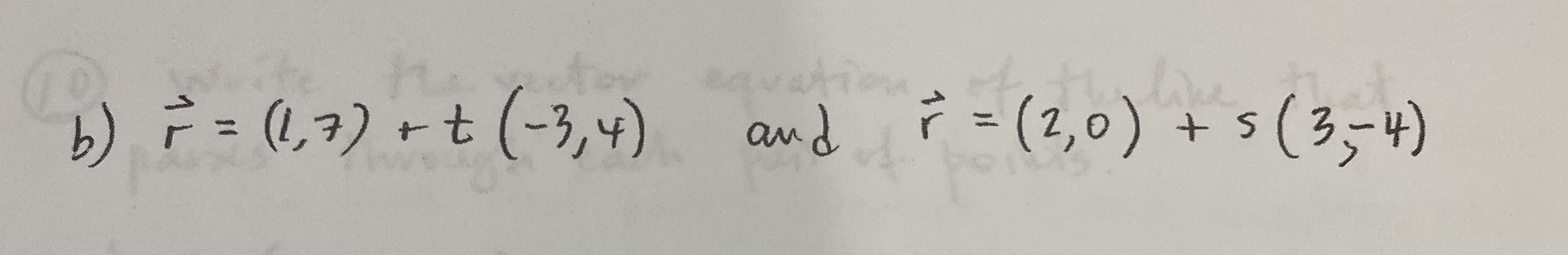
Write the parametric equations for each vector equation a ) [ x , y ] = [ - 2 , 1] + t [0, 2] 6 ) [xx, y] = [3, 7] + + [- 2, -5] (3) Determine if point P is on the line. P = (- 14, 15 ) (x = 1+ 3+ telR Ty = 5 -2t4 Write a vector equation for each live, given the parametric equations "x = - 2 + 4t a ) l: 2 4 = 3 - 5t b ) R: 1 x = - 9t y = 8 + 3 t (5) Given each set of parametric equations, write the scalar equation. a ). * = 2+ 3 + R: 14 = = 2 -4t b) R: 5 x = 3 + 8+ 4 = - 4 + 7 t16. Write the scalar equation of each like given the normal vecter n and point Po. a ) n = 15, 2 ], 80 ( 1 , - 6 ) 6) n = [2, - 31, Po (5, 2) 7. Find a vector equation of the like That passes through the point ( 4, 5) and is perpendicular to the like ? = (1,8 ) + t (3, 7 )8) For each of The following, determine which pairs of likes are parallel and which are perpendicular. a) x = 1 - 3t, 4= 7+4t and x= 2-4s, y= -3x
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


