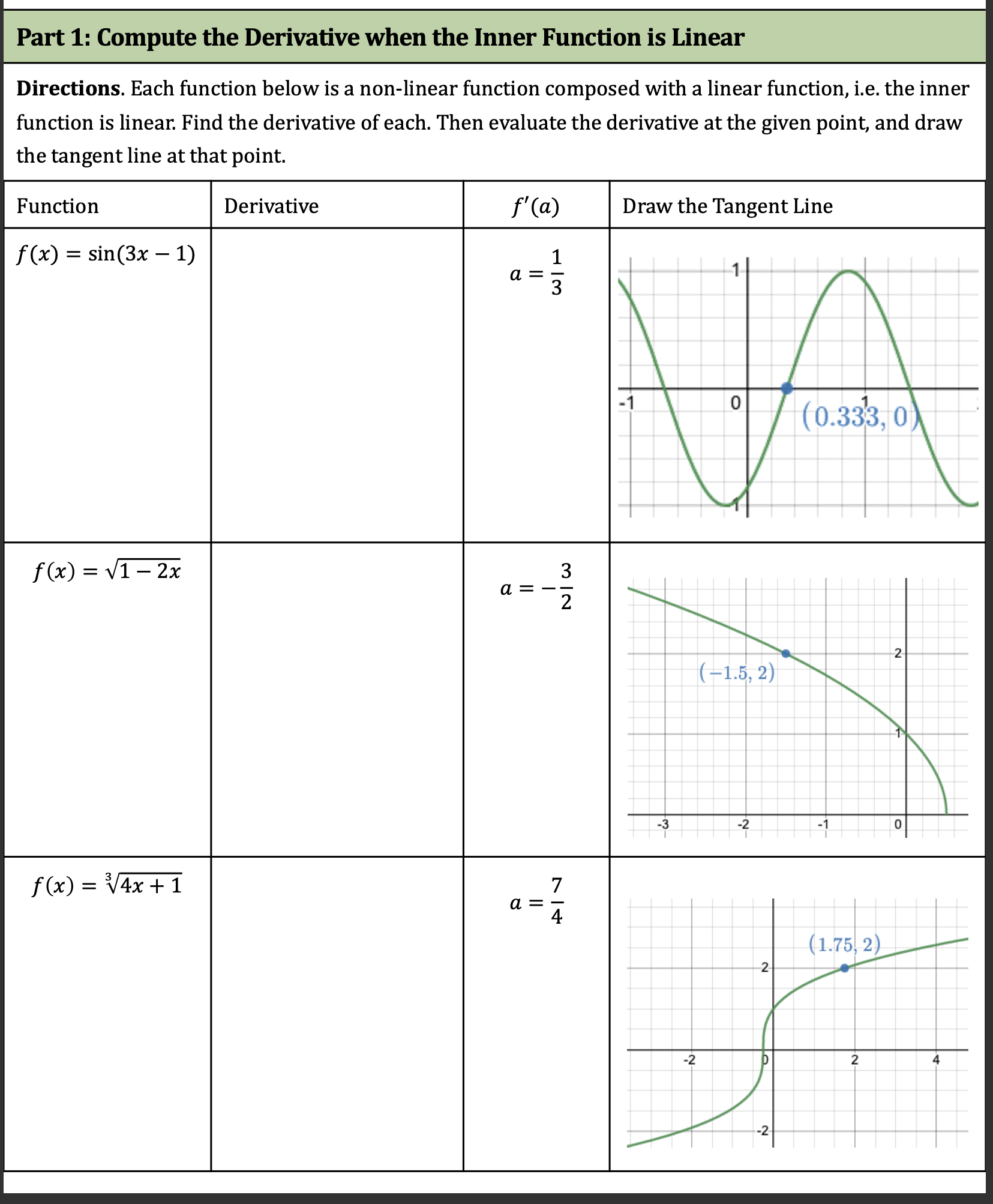
Question: Calculus: Part 1: Compute the Derivative when the Inner Function is Linear Directions. Each function below is a non-linear function composed with a linear function,

Calculus:
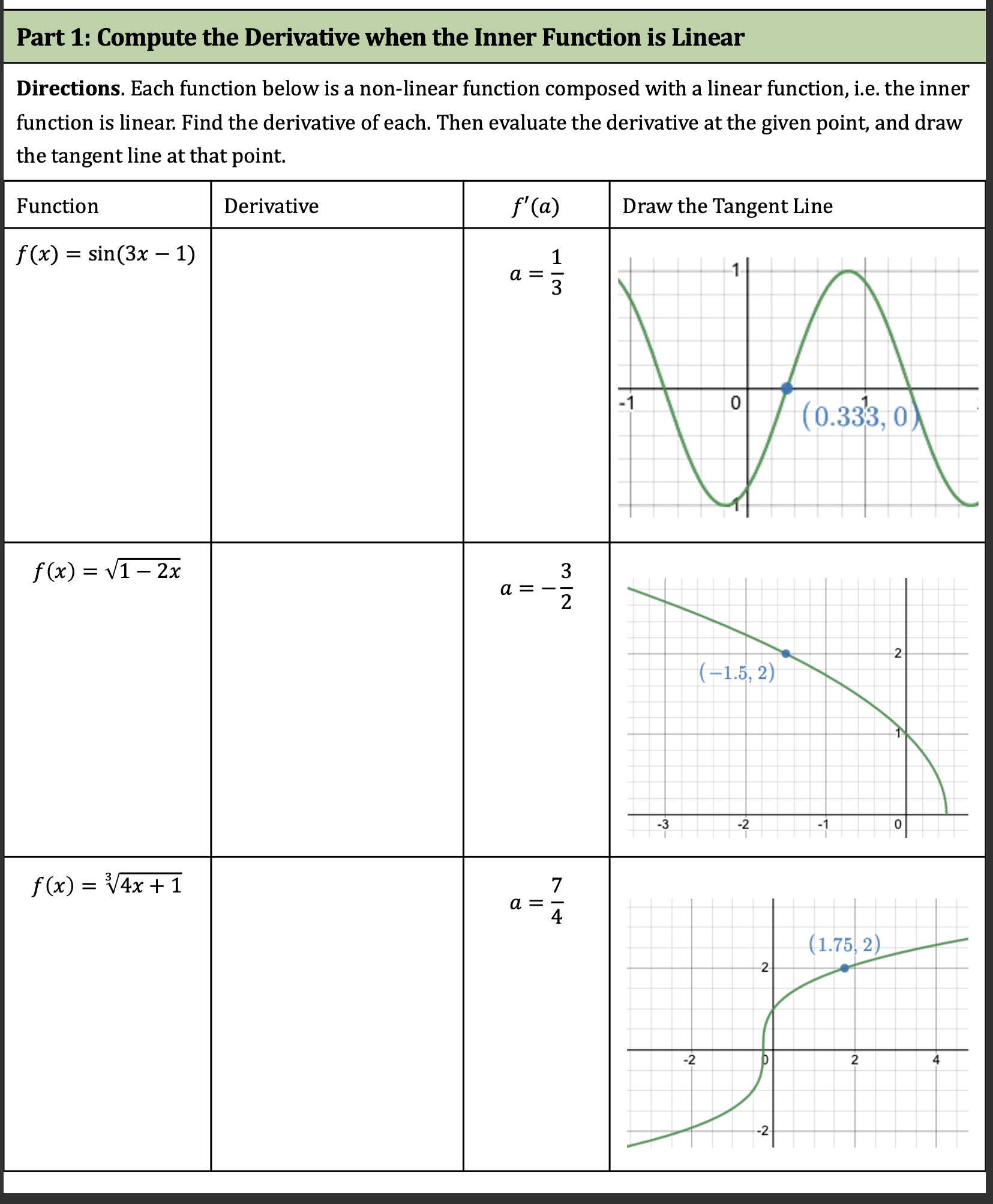
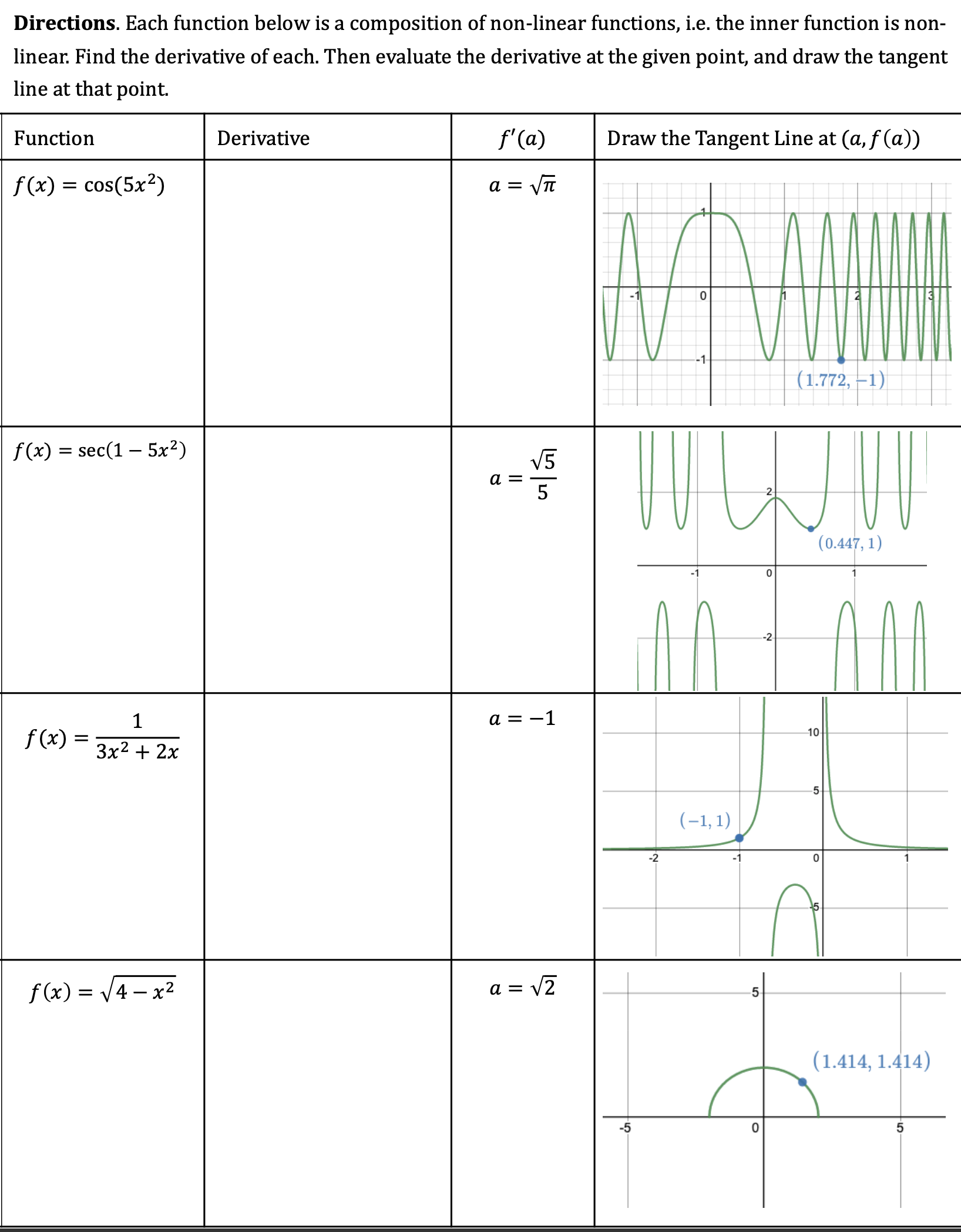

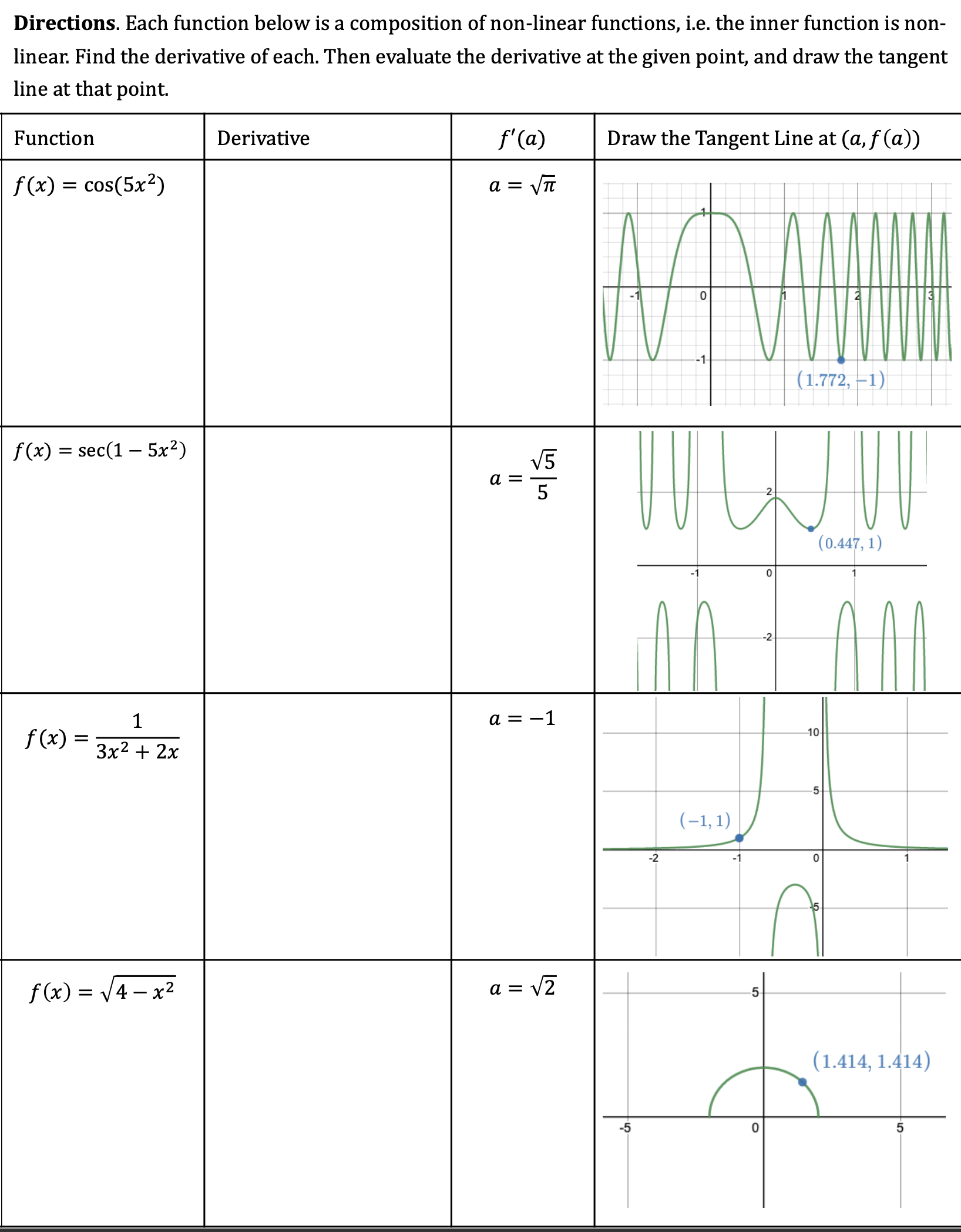
Part 1: Compute the Derivative when the Inner Function is Linear Directions. Each function below is a non-linear function composed with a linear function, i.e. the inner function is linear. Find the derivative of each. Then evaluate the derivative at the given point, and draw the tangent line at that point. f(x) sin(3x 1) Directions. Each function below is a composition of non-linear functions, i.e. the inner function is non- linear: Find the derivative of each. Then evaluate the derivative at the given point, and draw the tangent line at that point. f(x) = cos(5x2) f(x) = sec(1 5x2) [04-17, 1) 1'00 = 3x2 + 2x Directions. Find each derivative below. Each will require more than one rule (product, quotient, chain). Simplify your final answers. [Factor out GCFs where possible). xS (22c+1)2 L fa): z f@)=smtV53t
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


