Can any one help me handle this data science question? thanks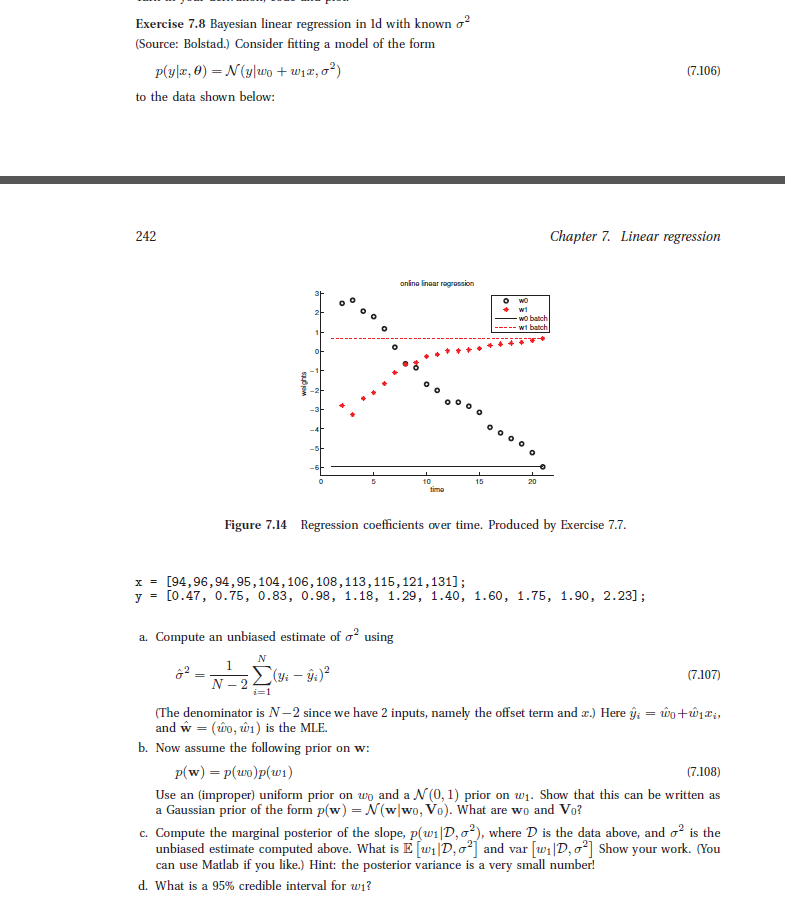

Exercise 7.8 Bayesian linear regression in Id with known 2 (Source: Bolstad.) Consider fitting a model of the form (7.106) to the data shown below: 242 Chapter 7. Linear regression onina Inoar rograssiorn _Wo batch wi batch Figure 7.14 Regression coefficients over time. Produced by Exercise 7.7 [94,96 ,94,95 , 104,106 , 108,113 , 115,121,131] ; [0.47, 0.75, 0.83, 0.98, 1.18, 1.29, 1.40, x= y 1.60, 1.75, 1.90, 2.23]; a. Compute an unbiased estimate of 2 using 7.107) (The denominator is N-2 since we have 2 inputs, namely the offset term and r.) Here ywi, and w - (wo, wi) is the MLE. Now assume the following prior on w: b. p(w)p(wo)p(wi) (7.108) Use an (improper) uniform prior on wo and a N(0,1) prior on w. Show that this can be written as a Gaussian prior of the forn p(w) = N(wlwo,Vo), what are wo and Vo? c. Compute the marginal posterior of the slope, p uip,02), where D is the data above, and 2 is the unbiased estimate computed above. What is E [w|D, 2] and var [w1D, 2] Show your work. (You can use Matlab if you like.) Hint: the posterior variance is a very small number! d. What is a 95% credible interval for w Exercise 7.8 Bayesian linear regression in Id with known 2 (Source: Bolstad.) Consider fitting a model of the form (7.106) to the data shown below: 242 Chapter 7. Linear regression onina Inoar rograssiorn _Wo batch wi batch Figure 7.14 Regression coefficients over time. Produced by Exercise 7.7 [94,96 ,94,95 , 104,106 , 108,113 , 115,121,131] ; [0.47, 0.75, 0.83, 0.98, 1.18, 1.29, 1.40, x= y 1.60, 1.75, 1.90, 2.23]; a. Compute an unbiased estimate of 2 using 7.107) (The denominator is N-2 since we have 2 inputs, namely the offset term and r.) Here ywi, and w - (wo, wi) is the MLE. Now assume the following prior on w: b. p(w)p(wo)p(wi) (7.108) Use an (improper) uniform prior on wo and a N(0,1) prior on w. Show that this can be written as a Gaussian prior of the forn p(w) = N(wlwo,Vo), what are wo and Vo? c. Compute the marginal posterior of the slope, p uip,02), where D is the data above, and 2 is the unbiased estimate computed above. What is E [w|D, 2] and var [w1D, 2] Show your work. (You can use Matlab if you like.) Hint: the posterior variance is a very small number! d. What is a 95% credible interval for w