Can anyone help me with this in python? Theres one file i can edit(main.py) and another i cant and that im supposed to call to(pendulum.py) in order to make the code work. Any help would be greatly appreciated!

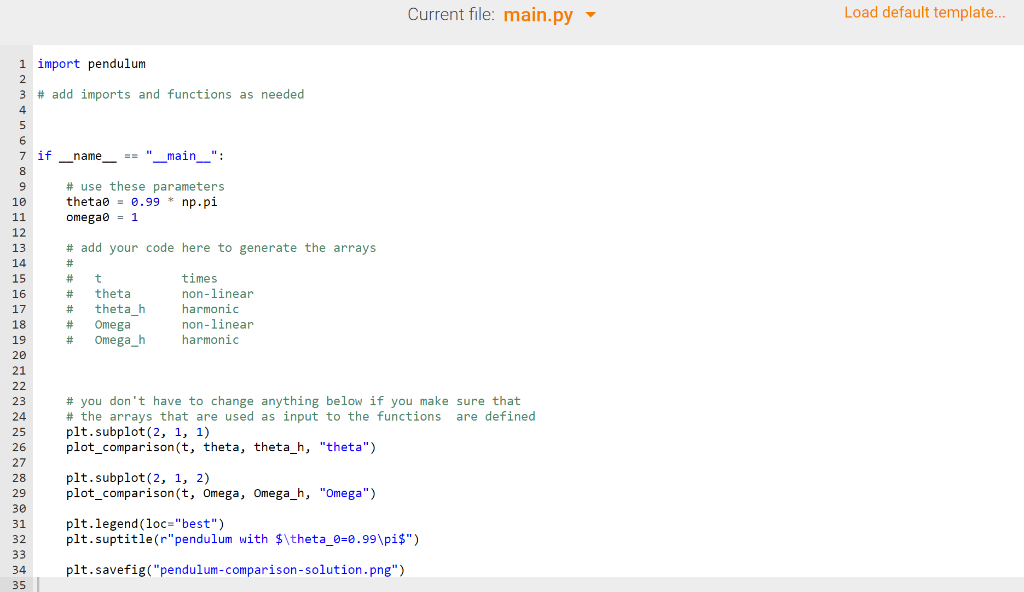
Harmonic pendulum analytical solution Write functions to generate angles and angular velocity time series: 1. The function harmonic_theta(t, thetao, omega=1) should return the angle (t) for the input array of times t and the initial angular deflection thetao. The angular frequency should be an optional keyword argument with default 1. The function should return a numpy array containing the O(t). 2. The function harmonic_Omega(t, thetao, omega0=1) should return the angular velocities 2(t) for the input array of times t and the initial angular deflection thetao. The angular frequency should be an optional keyword argument with default 1 and a numpy array should be returned. Plotting Write a function plot_comparison(t, x, xharmonic, ylabel) that takes as input . t: a numpy array to times; x: a numpy array of observables for the non-linear pendulum. The parameter x can be set to either an array of angles or angular velocities; xharmonic: a numpy array of observables for the harmonic pendulum (see x) ylabel: a string that is used to label the y-axis, should be either "theta" or "Omega", depending on what was chosen for x and xharmonic It should plot the non-linear and the harmonic timeseries in the same axes, create legends "non-linear" and "harmonic" for the graphs, . add the label "time" to the x-axis, add the ylabel to the y-axis. Current file: main.py Load default template... 1 import pendulum 2 3 # add imports and functions as needed 4 _name__ == "_main__": # use these parameters thetab = 0.99 * np.pi omegao = 1 # add your code here to generate the arrays # # t times # # theta non-linear # theta h harmonic # Omega non-linear # Omega_h harmonic 5 6 7 if 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 23 24 25 26 27 28 29 30 31 32 33 34 35 # you don't have to change anything below if you make sure that # the arrays that are used as input to the functions are defined plt. subplot(2, 1, 1) plot_comparison(t, theta, theta_h, "theta") plt. subplot(2, 1, 2) plot_comparison(t, Omega, Omega_h, "Omega") plt.legend (loc="best") plt.suptitle(r"pendulum with $\theta_0=0.99\pis") plt. savefig("pendulum-comparison-solution.png") File is marked as read only Current file: pendulum.py 1 # integration of the equations of motion of the non-linear pendulum with the Euler integrator 2 3 import numpy as np 4 5 # parameters 6 default_omega0 = 1 7 8 def integrate(thetao, dt=0.01, nmax=5, omegao=default_omegao): 9 "'"Integrate the non-linear pendulum with Euler. Parameters 1 -2 3 4 5 -6 -7 -8 9 thetan: float initial angular displacement (in radians) dt : float integrator time step nmax : float or int number of harmonic periods TO = 21/omegao for which the trajectory is sampled. omega : float angular frequency of the harmonic pendulum -1 -2 -3 -4 -5 Returns -7 -8 array The array has shape (3, N) where N is the number of time steps and the three rows correspond to time, theta, Omega time series. Note The initial angular velocity is set to o, i.e., the pendulum always starts from rest and the largest deflection is thetae. omega2 = omegao**2 TO = 2*np.pi/omega Tmax = nmax * TO # pre-compute the square # harmonic period # max sampling time # print (f"TO = {TO}, Tmax = {Tmax}") 0 -1 2 3 4 5 6 7 8 9 0 -1 -2 -3 -4 -5 -6 -7 -8 -9 0 1 -2 -3 -4 5 theta = thetao Omega = 0 # always start from rest t = 0 data = [(t, theta, Omega)] # record initial condition while t