Can anyone write a Python programme for the following question?

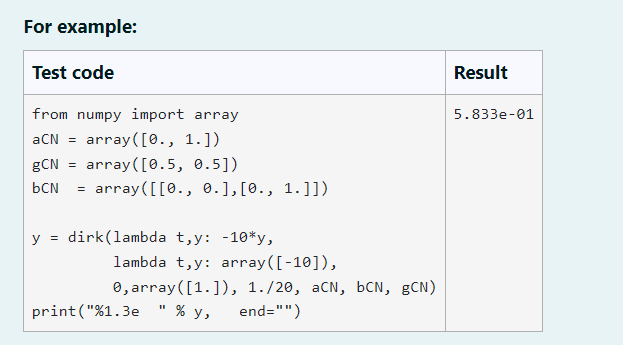
Write a function that performs one step of a general s-stage diagonally implicit Runge-Kutta method to a vector valued nonhomogeneous ODE: y(t)=f(t,y(t)) In addition to the usual y0,t0 the step size h and the right hand side f with its Jacobian with respect to the y component (needed for Newton's method) the user also needs to provide the two vectors , and the matrix making up the Butcher tableau of the RungeKutta method. You can assume that has only zero entries above the diagonal since we are only looking at diagonally implicit RK methods. Function template Python def dirk(f,Df, to,y0, h, alpha,beta,gamma): \# your code to compute y return y Remark: I'm using 1e15 as tolerance for the Newton method - the O(h2) I suggested for the BE method might not be good enough for higher order methods. For example