Can i have help with python3?

Now you will create a class which will hold a list of points, and potentially the equation of a line which contains all these points.

Define a class named LineEquation with an appropriate __init__ method. The __init__ method has one optional parameter named points. This class has two attributes: a list of points, named points, and a string which will hold the equation of a line, named line_equation. In the event that a list of points was provided during the creation of a LineEquation object, set the points attribute to the list sent in, otherwise set points to be an empty list. Set the line_equation attribute of the class to be the string "No straight line solution possible". Then, call your class method find_line_equation to update your line_equation attribute. You might not have implemented the find_line_equation method yet, but don't worry, we'll get to that shortly.

Implement the __repr__ method for your class. This method returns exactly what you would need to type if you were to recreate this object. See the doctests below for example output.

Implement the __str__ method for your class. This method is intended to be more "human-readable" and returns the list of points, a newline character, and the line equation. See the doctests below for examples of what the __str__ method returns when a LineEquation object is printed.

We have arrived at the point(!) of this whole endeavor. It is time to find the equation of a straight line (if there is one) which joins all our points together and update the line_equation attribute of our object. For the sake of simplicity, you may assume that no collection of points will produce a vertical line. Implement a method named find_line_equation. Here are the steps:

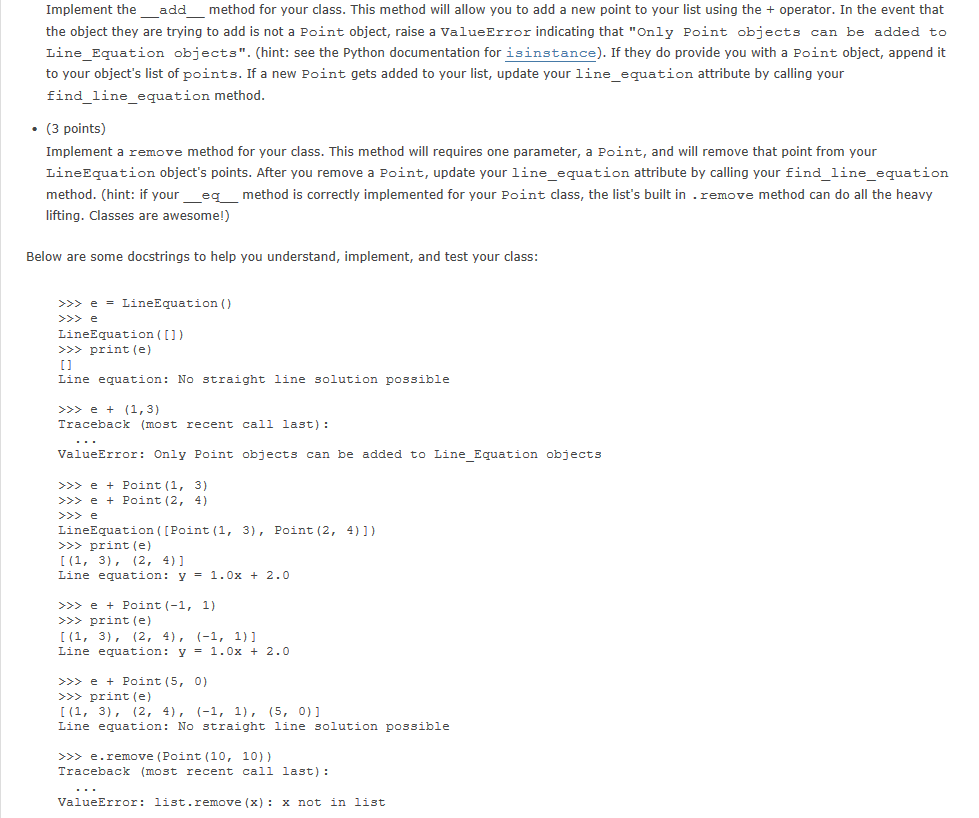
Implement the __add__ method for your class. This method will allow you to add a new point to your list using the + operator. In the event that the object they are trying to add is not a Point object, raise a ValueError indicating that "Only Point objects can be added to Line_Equation objects". (hint: see the Python documentation for isinstance). If they do provide you with a Point object, append it to your object's list of points. If a new Point gets added to your list, update your line_equation attribute by calling your find_line_equation method.

Implement a remove method for your class. This method will requires one parameter, a Point, and will remove that point from your LineEquation object's points. After you remove a Point, update your line_equation attribute by calling your find_line_equation method. (hint: if your __eq__ method is correctly implemented for your Point class, the list's built in .remove method can do all the heavy lifting. Classes are awesome!)

(3 points)

(3 points)

(3 points)

(10 points)

If you have fewer than two points, there's no way to make a line. Update your object's line_equation attribute to "No straight line solution possible".

If your list of points contains exactly two points, finding the line is too easy. First, determine the slope using the slope formula:

m=(y2y1)(x2x1)m=(y2y1)(x2x1)

Then, use m from above with x and y from one of your points in the equation of a line and solve for b:

y=mx+by=mx+b

Or, written another way:

b=ymxb=ymx

Now, you know m and b, so update the line_equation attribute of our object to be the string y = mx + b, where m and b are what was just calculated. When creating the string y = mx + b, round m and b to 2 decimal places.

If we have more than 3 points, it gets a little tricky. First, pick two points from your list of points and perform the above procedure to determine the equation of a line which fits them. (hint: I used a sorted list of my points and grabbed the first two. This is possible because we overloaded the __lt__ method for our Point class! Amazing, isn't it!). Then, check if all the points on your line satisfy that equation. If they do, update the line_equation attribute of our object to be the string y = mx + b. If any Point fails to satisfy your discovered equation, update the line_equation attribute to "No straight line solution possible".

(3 points)

(3 points)

Below are some docstrings to help you understand, implement, and test your class:

 >>> e = LineEquation() >>> e LineEquation([]) >>> print(e) [] Line equation: No straight line solution possible >>> e + (1,3) Traceback (most recent call last): ... ValueError: Only Point objects can be added to Line_Equation objects >>> e + Point(1, 3) >>> e + Point(2, 4) >>> e LineEquation([Point(1, 3), Point(2, 4)]) >>> print(e) [(1, 3), (2, 4)] Line equation: y = 1.0x + 2.0 >>> e + Point(-1, 1) >>> print(e) [(1, 3), (2, 4), (-1, 1)] Line equation: y = 1.0x + 2.0 >>> e + Point(5, 0) >>> print(e) [(1, 3), (2, 4), (-1, 1), (5, 0)] Line equation: No straight line solution possible >>> e.remove(Point(10, 10)) Traceback (most recent call last): ... ValueError: list.remove(x): x not in list >>> e.remove(Point(5, 0)) >>> print(e) [(1, 3), (2, 4), (-1, 1)] Line equation: y = 1.0x + 2.0 >>> e2 = LineEquation([Point(-5, 0), Point(0, 5)]) >>> print(e2) [(-5, 0), (0, 5)] Line equation: y = 1.0x + 5.0 >>> e2 = LineEquation([Point(-5, 0), Point(0, 5)]) >>> print(e2) [(-5, 0), (0, 5)] Line equation: y = 1.0x + 5.0 >>> e3 = LineEquation([Point(-2, 8), Point(-1, 0)]) >>> print(e3) [(-2, 8), (-1, 0)] Line equation: y = -8.0x + -8.0 >>> e4 = LineEquation([Point(-3, -2), Point(1, 1)]) >>> print(e4) [(-3, -2), (1, 1)] Line equation: y = 0.75x + 0.25 

Now you will create a class which will hold a list of points, and potentially the equation of a line which contains all these points . (3 points) Define a class named LineEquation with an appropriate init method. The init method has one optional parameter named p ints. This class has two attributes: a list of points, named points, and a string which will hold the equation of a line, named line_equation. In the event that a list of points was provided during the creation of a LineEquation object, set the points attribute to the list sent in, otherwise set p ints to be an empty list. Set the line-equati n attribute of the class to be the string "N straight line solution possible". Then, call your class method find_line_equation to update your line_equation attribute. You might not have implemented the find_line_equation method yet, but don't worry, we'll get to that shortly . (3 points) Implement the reprmethod for your class. This method returns exactly what you would need to type if you were to recreate this object. See the doctests below for example output. . (3 points) Implement the str method for your class. This method is intended to be more "human-readable" and returns the list of points, a newline character, and the line equation. See the doctests below for examples of what the str method returns when a LineEquation object is printed . (10 points) We have arrived at the point(!) of this whole endeavor. It is time to find the equation of a straight line (if there is one) which joins all our points together and update the line_equation attribute of our object. For the sake of simplicity, you may assume that no collection of points will produce a vertical line. Implement a method named find_line_equation. Here are the steps 1. If you have fewer than two points, there's no way to make a line. Update your object's line_equation attribute to "No straight line solution possible" 2. If your list of points contains exactly two points, finding the line is too easy. First, determine the slope using the slope formula: (y2 -) Then, use m from above with x and y from one of your points in the equation of a line and solve for b: Or, written another way: Now, you know m and b, so update the line-equation attribute of our object to be the string y = mx + b, where m and b are what was just calculated, when creating the string y = mx + b, round m and b to 2 decimal places 3. If we have more than 3 points, it gets a little tricky. First, pick two points from your list of points and perform the above procedure to determine the equation of a line which fits them. (hint: I used a sorted list of my points and grabbed the first two. This is possible because we overloaded the lt method for our Point class! Amazing, isn't it!). Then, check if all the points on your line satisfy that equation. If they do, update the line-equation attribute of our object to be the string y mx + b. If any Point fails to satisfy your discovered equation, update the line_equation attribute to "No straight line solution possible