Can someone explain finding the acceleration?

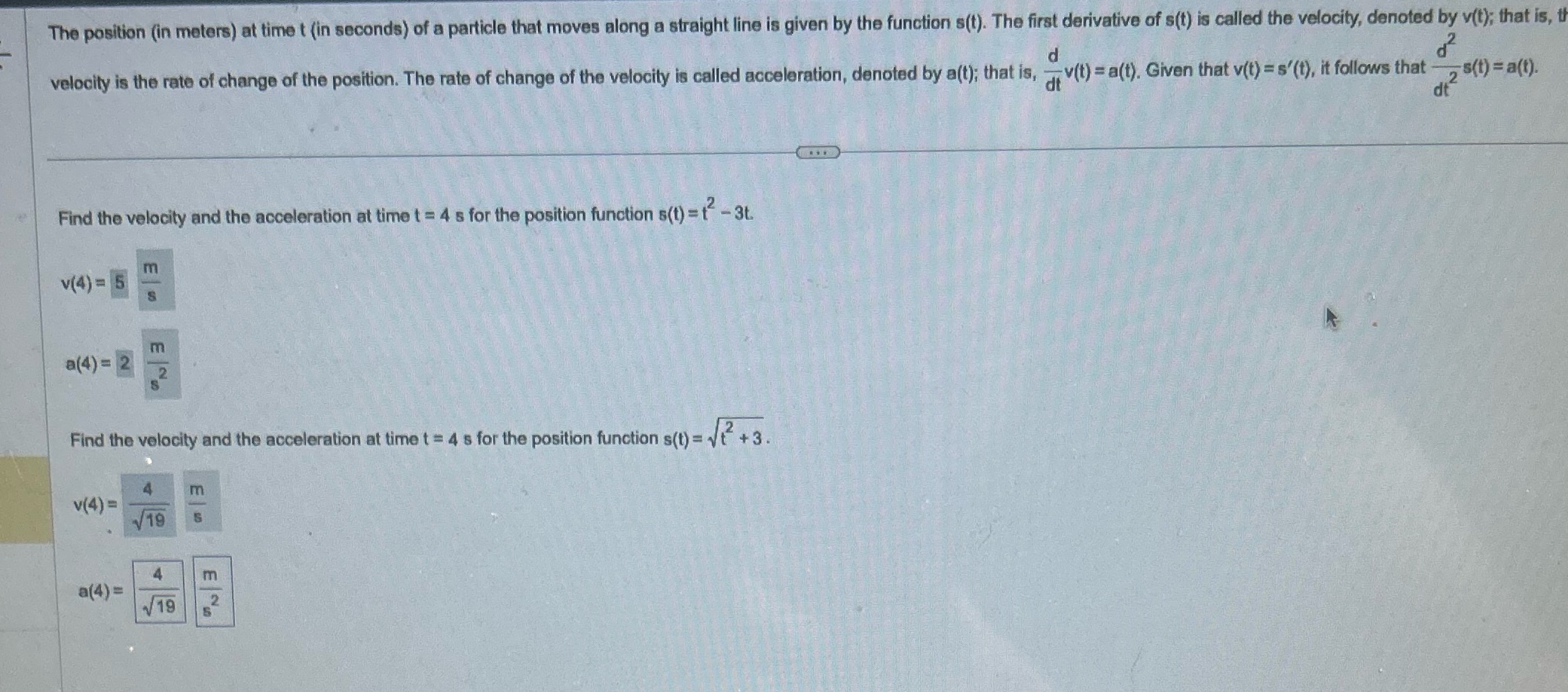
The position (in meters) at time t (in seconds) of a particle that moves along a straight line is given by the function s(t). The first derivative of s(t) is called the velocity, denoted by v(t); that is, the velocity is the rate of change of the position. The rate of change of the velocity is called acceleration, denoted by a(t); that is, -v(t) = a(t). Given that v(t) = s'(t), it follows that d+ 2 s(t) = a(t). Find the velocity and the acceleration at time t = 4 s for the position function s(t) = 2 - 3t. v(4) = 5 m a(4) = 2 m 2 Find the velocity and the acceleration at time t = 4 s for the position function s(t) = t +3. V(4)= m 19 TT a(4) = 19