Can someone help me, Please!

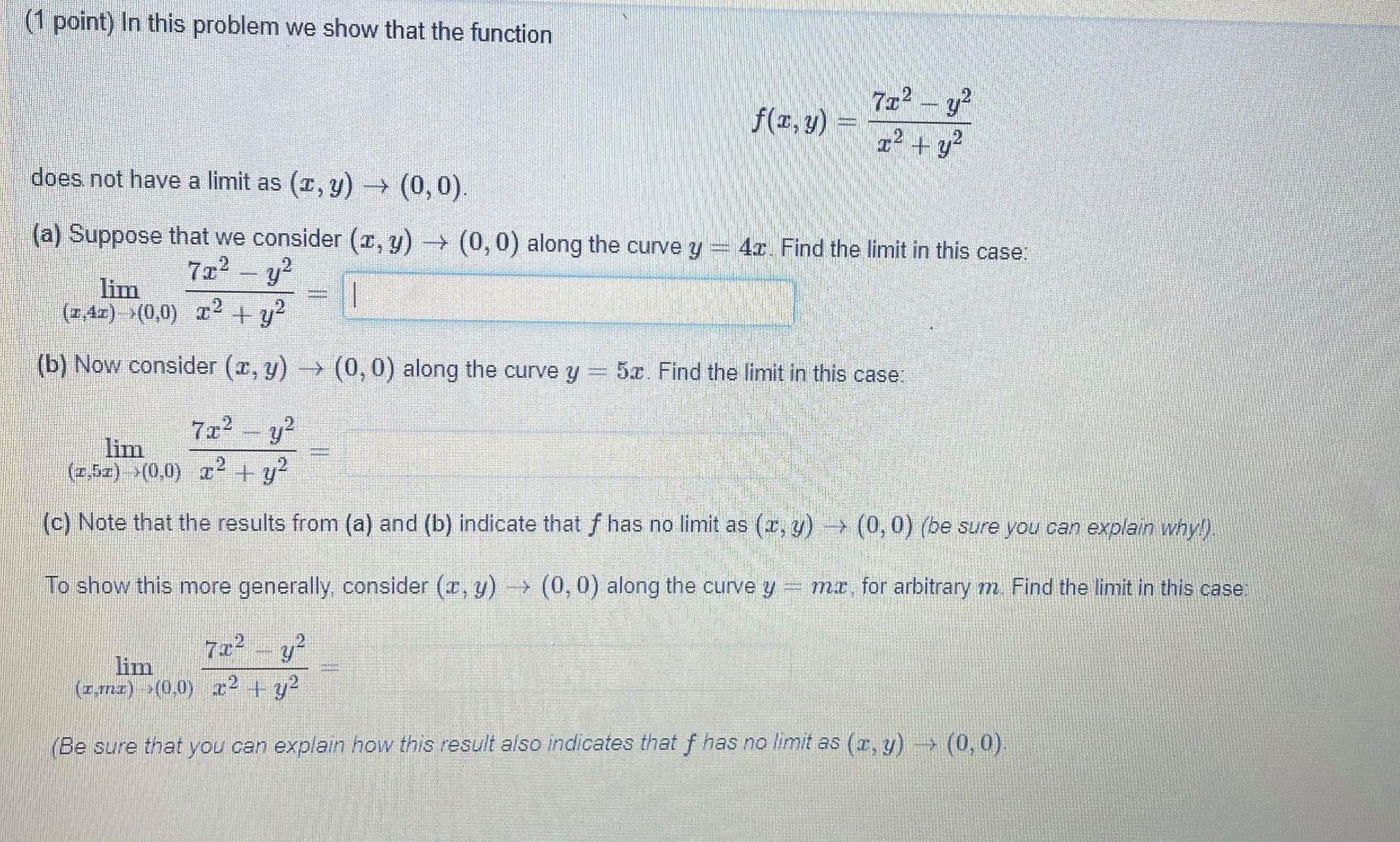
(1 point) In this problem we show that the function 712- 32 f ( I, y) 12 + 12 does not have a limit as (z, y) -> (0,0). (a) Suppose that we consider (z, y) -> (0, 0) along the curve y = 4x. Find the limit in this case: lim 72 - y2 (2,42) >(0.0) 2:2 72 (b) Now consider (z, y) -> (0, 0) along the curve y = 5.. Find the limit in this case: 712 - y2 lim (z,52) (0,0) x2+ 92 (c) Note that the results from (a) and (b) indicate that f has no limit as (a, y) -> (0, 0) (be sure you can explain why!). To show this more generally, consider (x, y) -> (0, 0) along the curve y - ma, for arbitrary m. Find the limit in this case. 722 - yz lim (z,ma) >(0,0) :2 4 3/2 Be sure that you can explain how this result also indicates that f has no limit as (x, y) -> (0,0)