Can someone help me use Excel to solve this problem? I think it should be straight forward but I might be missing a step.

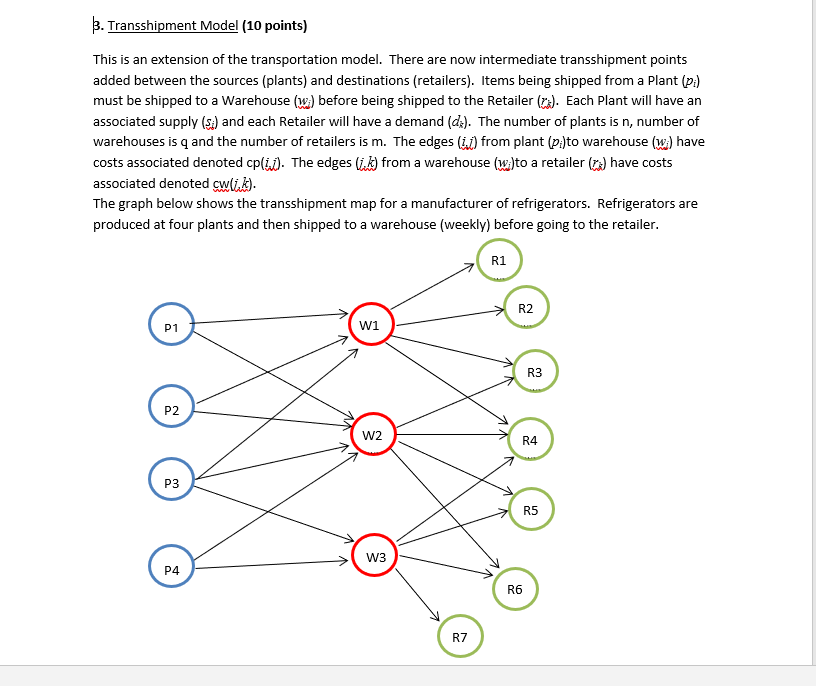
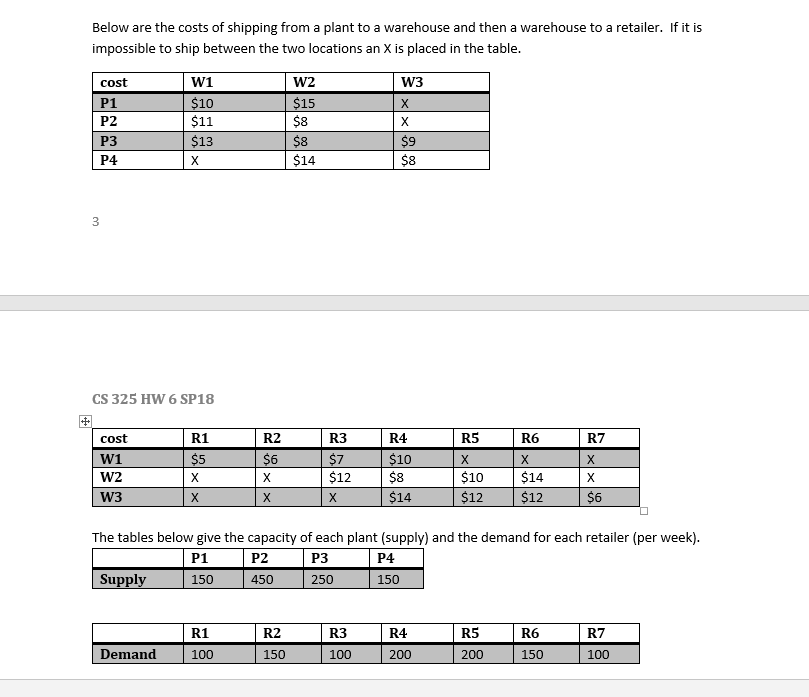
B. Transshipment Model (10 points) This is an extension of the transportation model. There are now intermediate transshipment points added between the sources (plants) and destinations (retailers). Items being shipped from a Plant (p) must be shipped to a aeose() before being shipped to the Retailer (z). Each Plant will have an associated supply (s) and each Retailer will have a demand (dk). The number of plants is n, number of warehouses is q and the number of retailers is m. The edges (G from plant (p)to warehouse (w) have costs associated denoted cp(). The edges )from a warehouse (w)to a retailer () have costs associated denoted cwli.) The graph below shows the transshipment map for a manufacturer of refrigerators. Refrigerators are produced at four plants and then shipped to a warehouse (weekly) before going to the retailer. R1 R2 W1 R3 P2 W2 R4 P3 R5 W3 P4 R6 R7 Below are the costs of shipping from a plant to a warehouse and then a warehouse to a retailer. If it is impossible to ship between the two locations an X is placed in the table cost P1 P2 P3 P4 W1 10 $11 $13 15 $8 $8 $14 $8 CS 325 HW 6 SP18 cost R1 R2 R3 R4 R5 R6 R7 W1 10 10 $14 $12 $12 $12 $8 $14 $6 The tables below give the capacity of each plant (supply) and the demand for each retailer (per week) P1 P3 250 P2 P4 150 450 150 R1 R2 R3 R4 R5 R6 R7 Demand 100 150 100 200 200 150 100 The tables below give the capacity of each plant (supply) and the demand for each retailer (per week) P1 P2 P3 P4. 150 450 250 150 R1 R2 R3 R4 R5 R6 R7 Demand 100 150 100 200 200 150 100 Part A: Determine the number of refrigerators to be shipped from the plants to the warehouses and then warehouses to retailers to minimize the cost. Formulate the problem as a linear program with an objective function and all constraints. Determine the optimal solution for the linear program using any software you want. What are the optimal shipping routes and minimum cost? Part B: Due to old infrastructure Warehouse 2 is going to close eliminating all of the associated routes. What is the optimal solution for this modified model? Is it feasible to ship all the refrigerators to either warehouse 1 or 3 and then to the retailers without using warehouse 2? Why or why not? Part C: Instead of closing Warehouse 2 management has decide to keep a portion of it open but limit shipments to 100 refrigerators per week. Is this feasible? If so what is the optimal solution when warehouse 2 is limited to 100 refrigerators? Note: Include a copy of the code for all parts of the