Can someone please answer the following question using MATLAB language? Can you please comment your code and post a picture of part 1, that would be very helpful. I apologize for posting such a long question. I would post it as separate questions, but parts 2-4 are dependent on the correct answer to part 1. I have posted the incomplete codes for parts 3 & 4 below.

Here are some hints/tips:

% Problem 4: ODEsnd order ODE -> 2 initial conditions. (Given) % g ~ 10, l = 10. c will be varied. % You need to find f(z,t) - system of ODEs. % You need to set z(0) - initial condition. % z = [x y]'. % Can't do Parts 2, 3, and 4 without doing 1. % Part 2: ode45 can solve dz/dt = f(z,t) with z(0)- all of these must be computed from Part 1. % Rk4 - input arguments % RK4 - output arguments, it is returned by ode45. Then you have to calculate theta and dtheta - position and velocity. Think about how to extract this information from the output of ode45. % After integration, calculate energy in the pendulum. % You will calculate an initial energy e(0). % Energy at every timestep e(t). You have t and corresponding theta and % dtheta at each t from RK4. % theta 0 = pi/6 initially. % You should be able to generate those two plots for the two different % values of c. (use as a check) % Part 3: Calculate period. % When the event occurs for the 2nd time, that's when you will calculate % the period. Need to figure out what the "event" is. % Fill in what z and f are. % isterminal = 1. % position, direction - Need to figure out based on your "event" % Part 4: % Fill in the missing entries to visualize the simulation. % y - look at geometry to fill in the correct value. 

----------PART 3---------------

function [t] = period(T, theta0, reltol, abstol) % Period is the computed period for initial theta value theta0 (initial % omega value is always 0). % Simulation parameters: tspan = [0 T]; % Time interval of integration % Initial condition: z0 = ???; % System ODE dz/dt = f(z,t): f = ???; % Tolerance and event for detecting period of oscillation: options = odeset('abstol', abstol, 'reltol', reltol,'event',@EventsFcn); % Numerically integrate the IVP: [~,~,te,~,~] = ode45(f, tspan, z0, options); t = te(2); end function [position,isterminal,direction] = EventsFcn(t,z) position = ???; % The value that we want to be zero isterminal = ???; % Halt integration? 0 = false, 1 = true direction = ???; % Direction the zero can be approached: 0 = either, % +/-1 = event function is increasing/decreasng end

----------PART 4--------------

function animate_pendulum_e7 (T) % Numerical integration : z0 = ???; % Initial conditions f = ???; % System ODE dz/dt = f(z,t) reltol= 1e-8; abstol= 1e-8; % Tolerance [~, theta ,~] = RK4(f, z0 , T, reltol , abstol ); % Calculate the Cartesian coordinates (x,y) for the simple pendulum : y = ???; x = 10*sin(theta); % Figure properties : H = figure ('Name', 'Simple Pendulum ', 'Color', 'w'); anim = subplot (1 ,1 ,1); xlabel ('\itx') ylabel ('\ity', 'rotation', 0) set (anim , 'xlim', [-15 , 5] , 'ylim', [-15 , 5]) ; grid on; axis equal ; % Draw the pivot , initial position of pendulum and initial position of % mass bob at the end: rod = line ('xdata', [0 x(1)], 'ydata', [0 y(1)], 'color', 'r', 'linewidth', 2); mass = line ('xdata', x(1), 'ydata', y(1) , 'marker', 'o', 'color', 'r', 'markerfacecolor', 'r', 'linewidth', 4); pivot = line ('xdata', 0, 'ydata', 0, 'marker', '^', 'color','b', 'markerfacecolor', 'b', 'linewidth', 3); 

for k = 1: length (theta) set (rod , 'xdata', [0 x(k)] , 'ydata', [0 y(k)]); set (mass , 'xdata', x(k) , 'ydata',y(k)) ; drawnow end end

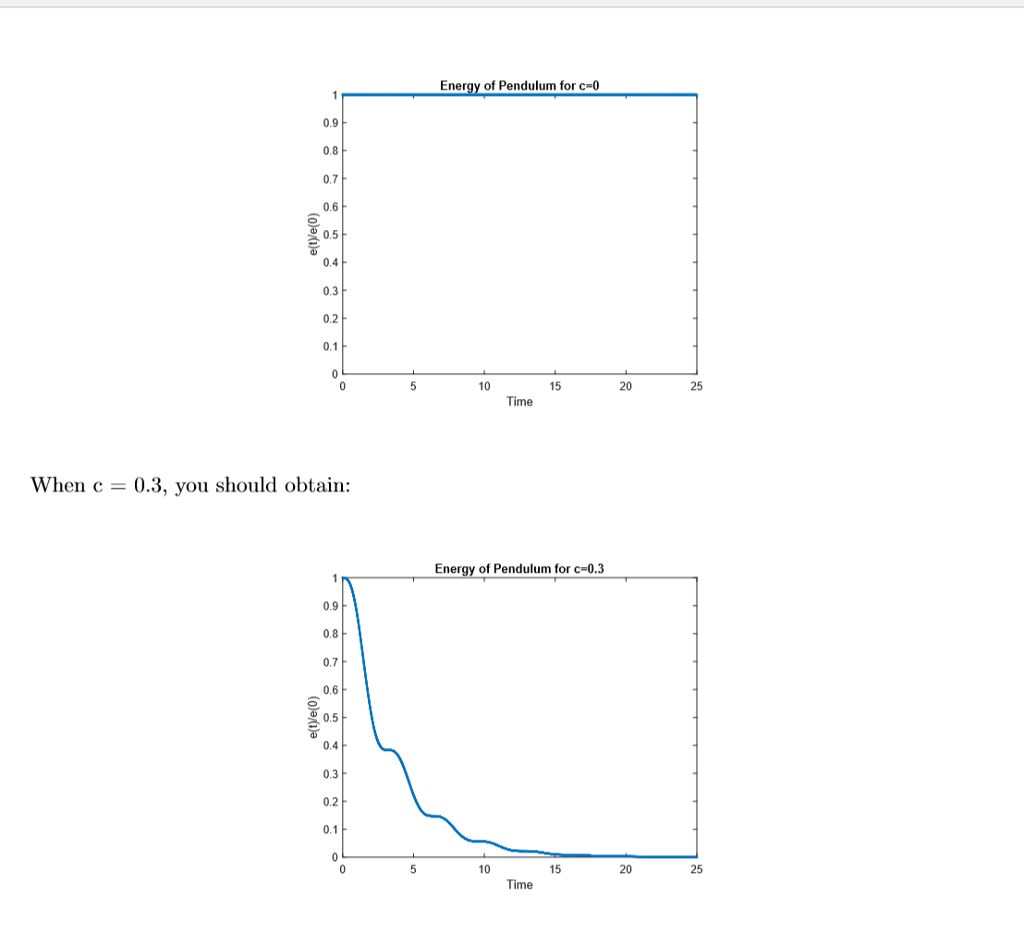
Homework Problem 4: Ordinary Differential Equations Consider a simple pendulum of length 1-10 m, forming an angle ?(t) with the vertical axis The equation of motion of the pendulum is given by 9 Assume g - the acceleration due to gravity - to be 10 m/s2 and c to be the damping constant. Consider the initial conditions di 1. Define a change of variables x-? and y = and write this systern in first-order form dr f2(x, y,t) where z = [x y]. Conpute the right hand side f(z,t), including z(0) Note: All of these calculations will be done on paper and do not have to be turned in, however you will use this information to write the code in subsequent parts hence is necessary 2. Use the information you calculated above to solve for ?(t) using MATLAB's built-in ode45 function To this effect, create a function RK4. Your function should solve the IVP dz/dt f(z,t) using ode45 RK4 should take in 5 input arguments- a) f - a function handle for the right hand side of Equation 8, b) z0 - a 2xl double array of initial conditions z0, c) T - the end time of integration, d) reltol - the relative error and e) abstol - the absolute error. The function should return 3 output arguments - t, theta and dtheta - which are three row arrays. After computing these three arrays, compute the pendulum's energy as a function of time. e(t)(1 - cos(0) Plot cas a function of time. (Think about what e(0) is). You should be able to reproduce the following two test cases Assume z0 is as calculated previously for this problem. Assume theta0= pi/6, abstol-le-12, reltol le-12 and T 25 When c 0 (no damping), you should obtain Homework Problem 4: Ordinary Differential Equations Consider a simple pendulum of length 1-10 m, forming an angle ?(t) with the vertical axis The equation of motion of the pendulum is given by 9 Assume g - the acceleration due to gravity - to be 10 m/s2 and c to be the damping constant. Consider the initial conditions di 1. Define a change of variables x-? and y = and write this systern in first-order form dr f2(x, y,t) where z = [x y]. Conpute the right hand side f(z,t), including z(0) Note: All of these calculations will be done on paper and do not have to be turned in, however you will use this information to write the code in subsequent parts hence is necessary 2. Use the information you calculated above to solve for ?(t) using MATLAB's built-in ode45 function To this effect, create a function RK4. Your function should solve the IVP dz/dt f(z,t) using ode45 RK4 should take in 5 input arguments- a) f - a function handle for the right hand side of Equation 8, b) z0 - a 2xl double array of initial conditions z0, c) T - the end time of integration, d) reltol - the relative error and e) abstol - the absolute error. The function should return 3 output arguments - t, theta and dtheta - which are three row arrays. After computing these three arrays, compute the pendulum's energy as a function of time. e(t)(1 - cos(0) Plot cas a function of time. (Think about what e(0) is). You should be able to reproduce the following two test cases Assume z0 is as calculated previously for this problem. Assume theta0= pi/6, abstol-le-12, reltol le-12 and T 25 When c 0 (no damping), you should obtain