Can someone please solve these 9 questions, please do not use chat gpt or any other source, and please if you use formulas only use the formula sheet I have provided. I will definitely give you a thumbs up if u follow this:) and please show work and all steps!! especially a lot for last 2 questions!!

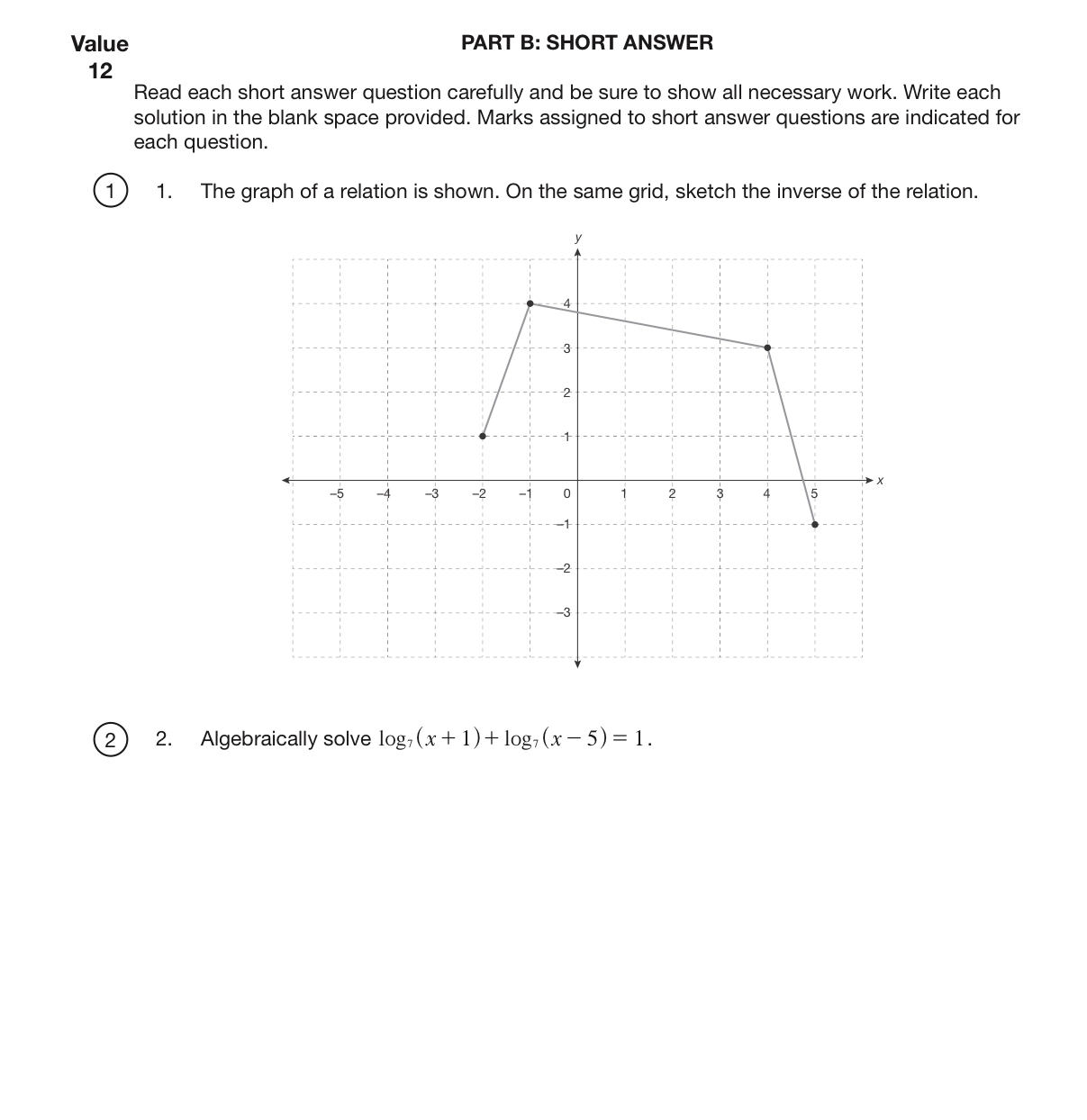
Mathematics 30-1 Formula Sheet For ax' + bx + c = 0, Trigonometry x = =bzyb - 4ac 2a 0 = a Relations and Functions tan 0 = sin 0 cot 0 = cos 0 cos 0 sin 0 Graphing Calculator Window Format csc 0 = - 1 1 sin 0 sec 0 = - cos 0 x: [Xmin, Xmax, Xsci ] cot 0 = 1 y: [ymin, ymax, ysci ] tan 0 Laws of Logarithms sin 0 + cos 0 = 1 1 + tan'0 = sec20 log. (M X N) = log,M + log.N 1 + cot20 = csc20 (M ) = log,M - log .N log. (M") = nlog.M sin (a + B) = sina cos B + cosa sin B logbc = log.C logab sin(a - B) = sin a cos B - cosa sin B cos (a + B) = cosa cos B - sin a sin B Growth/Decay Formula cos(a - B) = cosa cos B + sin a sin B y = abp tan (a + B) = tan a + tan B 1 - tan a tan B General Form of a Transformed Function tan (a - B) =- tana - tan B 1 + tan a tan B sin(2a) = 2 sin a cos a y = aflb(x - h) ]+ k cos(2a) = costa - sina Permutations, Combinations, cos (2a) = 2 costa - 1 and the Binomial Theorem cos (2a) = 1 - 2 sina tan(2a) = 2 tana n! = n(n - 1)(n - 2)...3 X 2 X 1, 1 - tan a where n E N and 0! = 1 y = asin[b(x - c)]+ d n! "P. =(n-r)! y = a cos[b(x - c)]+ d C,= n! (n - r)!r! "C, = (n) In the expansion of (x + y)", the general term is the 1 = " Ckx"-ky*.27. A total of 56 different two-item permutations can be created from a pile of clothes containing A. 8 garments B. 9 garments C. 10 garments D. 20 garments Numerical Response 11. The number of unique arrangements of all the letters in the word HISSIEST is 28. A committee of 5 is to be selected from 6 men and 5 women. If there must be at least 1 woman on the committee, the number of possible committees is A. 11 Cs - 6 C's B. SCI X 6 CA C. SC1 X 10 C4 D . s Cits C 2 + s C3 + s C+ + s C's 29. The number of ways 7 people can be selected to go on a trip from a class of 30 is A. 30 C7 B. 30 P7 C. 30! 7! D. 30!-23!30. At a meeting, each person shakes every other person's hand exactly once. If there are s handshakes in total, the number of people attending the meeting, m, can be determined using the equation A. m! = s B. m! - 2! - = S C. mP2 = S mC2 = s 31. The constant term in the expansion of the binomial ( + 2x) is A. B. 20 C. 160 D. 256 Numerical Response 12. If, when written in descending order by degree of x, the fourth term of (x + p ) is 4 320x], p is equal toValue PART B: SHORT ANSWER 12 Read each short answer question carefully and be sure to show all necessary work. Write each solution in the blank space provided. Marks assigned to short answer questions are indicated for each question. @ 1. The graph of a relation is shown. On the same grid, sketch the inverse of the relation. > o -2 -3 @ 2. Algebraically solve log; (x + 1)+ log:(x5) = 1