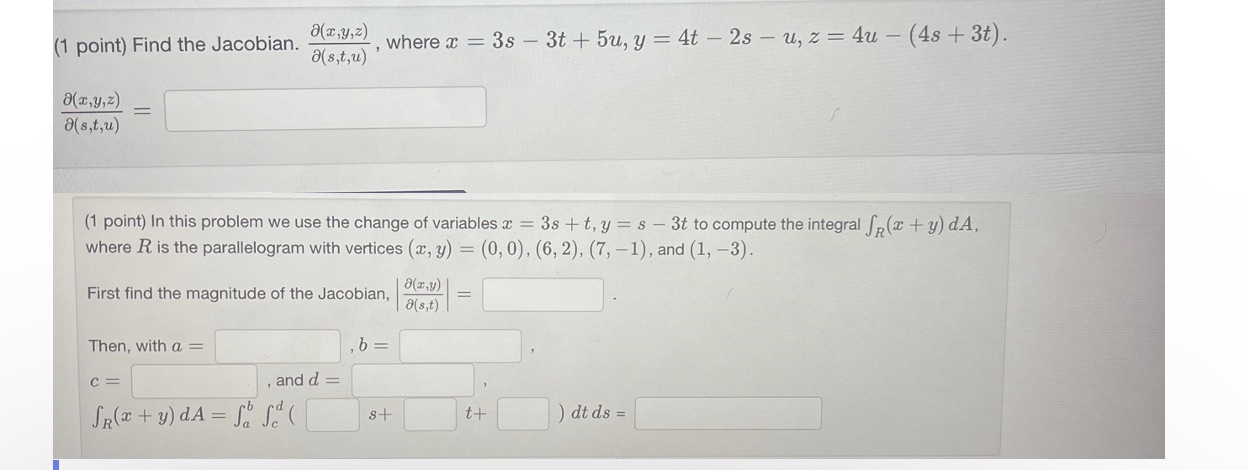
Question: Can someone solve this problem? o(x,y,z) (1 point) Find the Jacobian. , where c = 3s - 3t + 5u, y = 4t - 2s
Can someone solve this problem?
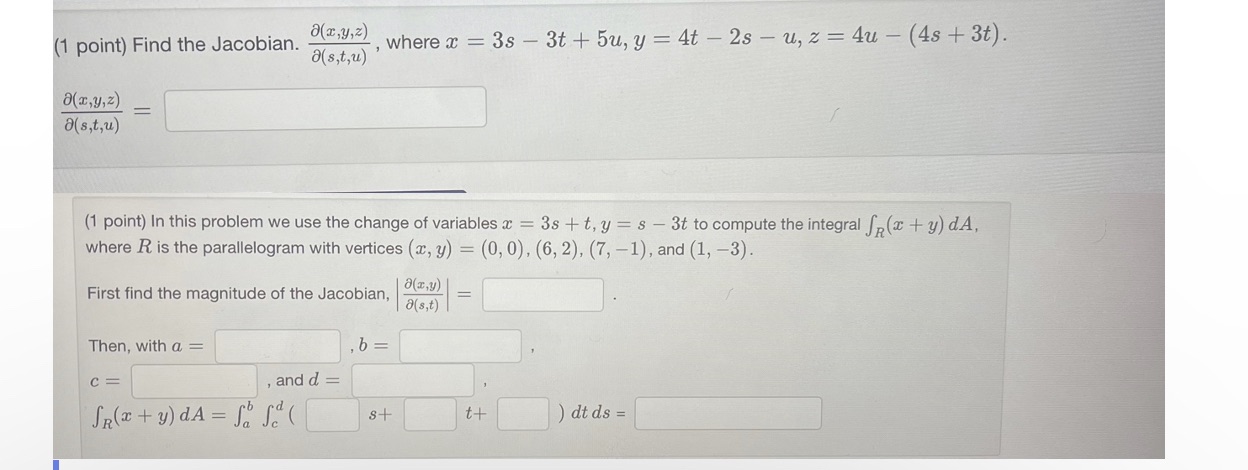
o(x,y,z) (1 point) Find the Jacobian. , where c = 3s - 3t + 5u, y = 4t - 2s - u, z = 4u - (4s + 3t). ( s, t, u) "(x , y, z) a( s, t, u ) (1 point) In this problem we use the change of variables x = 3s +t, y = s - 3t to compute the integral fp(x + y) dA, where R is the parallelogram with vertices (x, y) = (0, 0), (6, 2), (7, -1), and (1, -3). First find the magnitude of the Jacobian, a(x,y) a (s, t ) Then, with a = b C = , and d = SR(2 + y) dA = S& sa t+ ) dt ds =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


