Can someone troubleshoot my code?

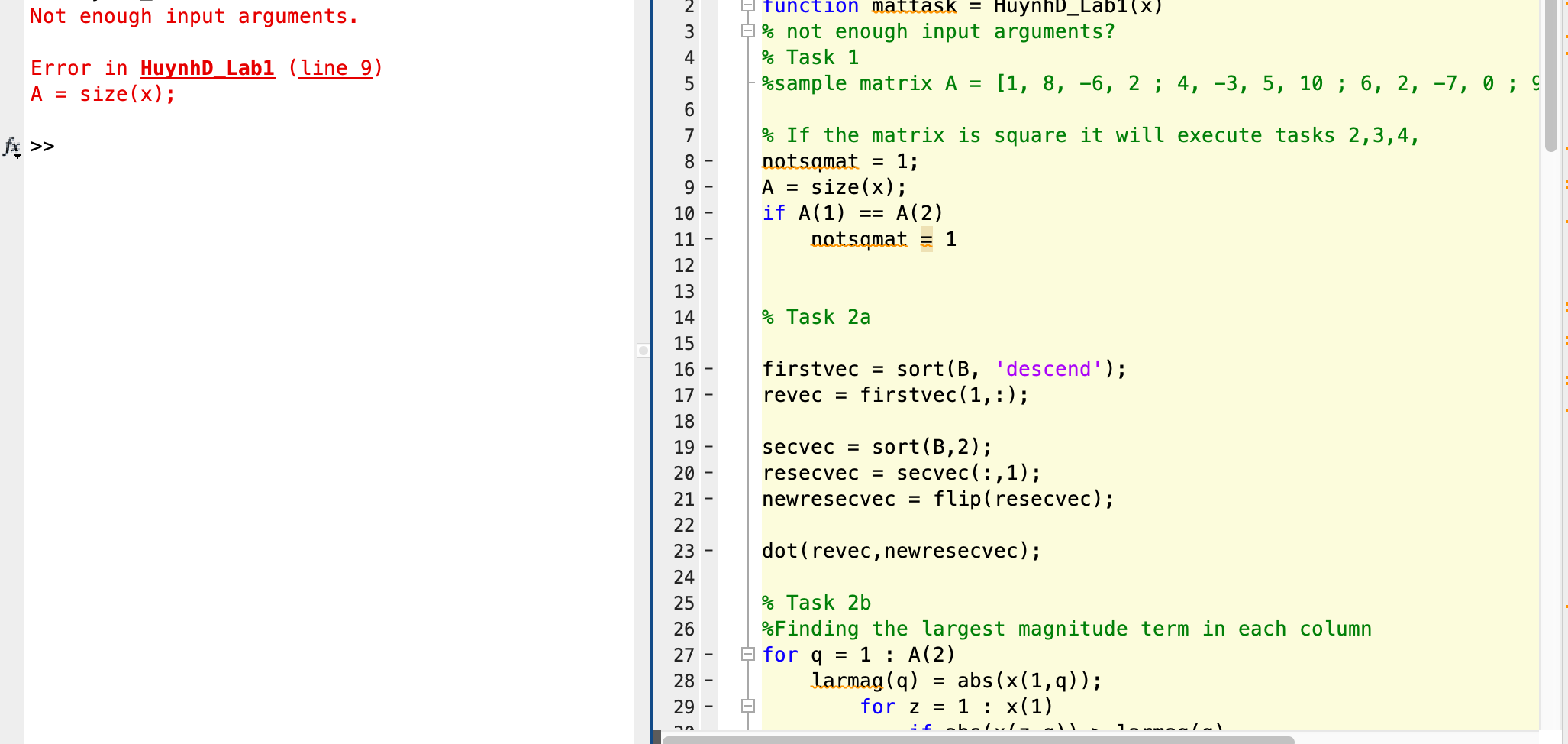
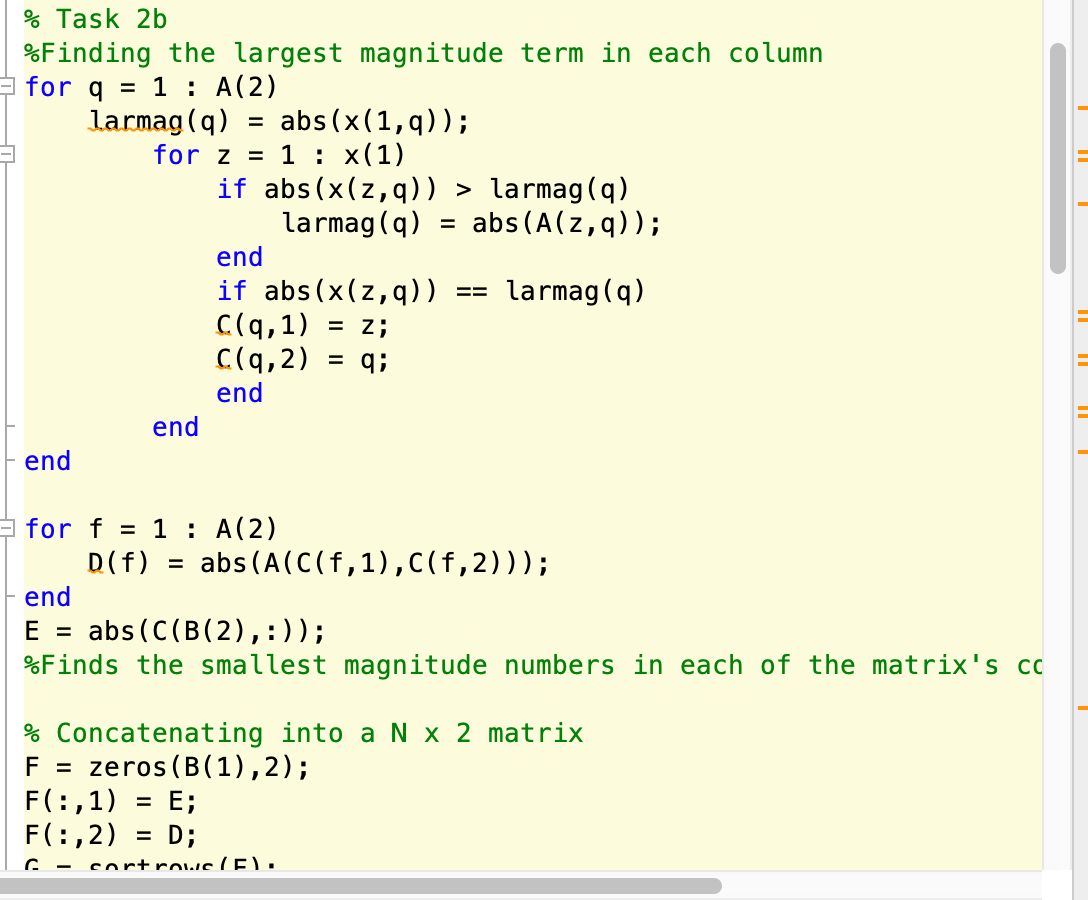
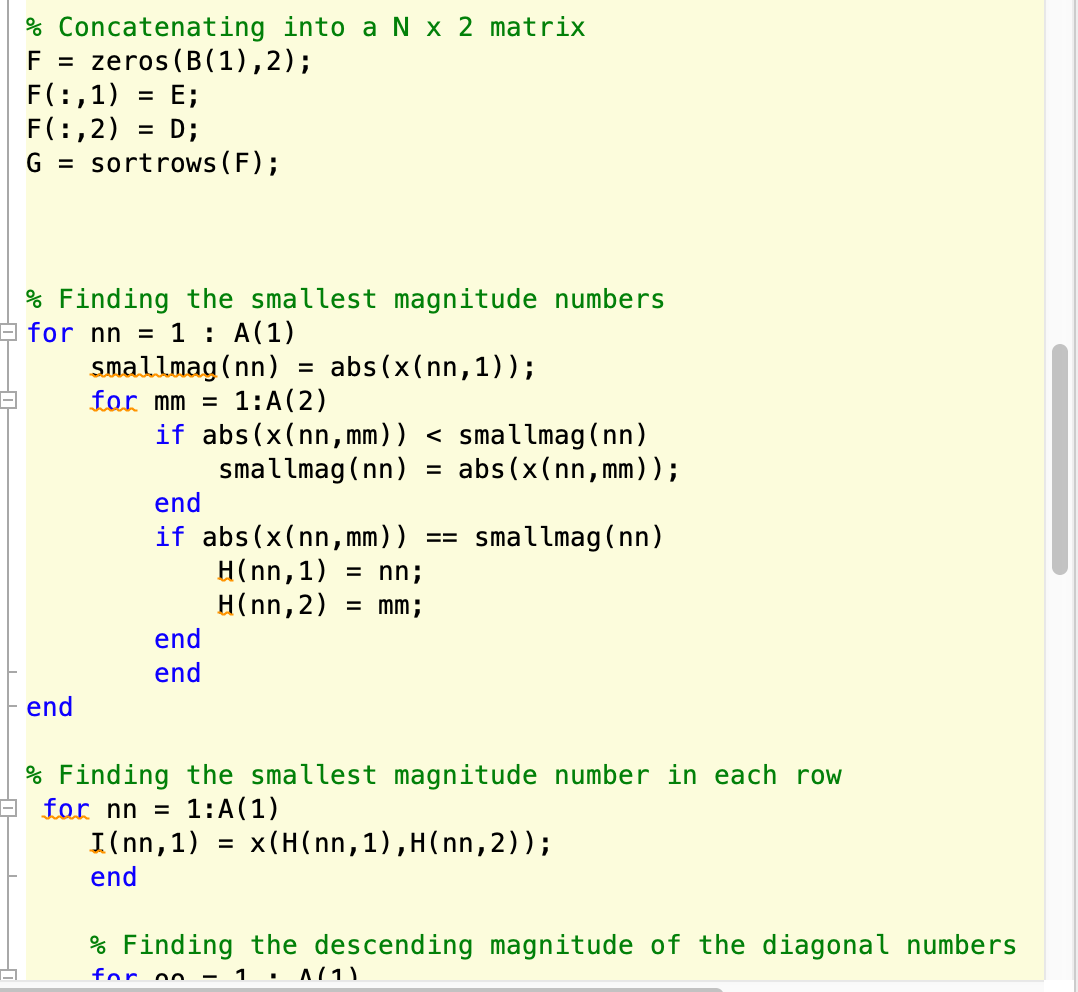
Not enough input arguments. 3 function mattask = HuynhD_Lab1(X) % not enough input arguments? % Task 1 :%sample matrix A = [1, 8, -6, 2; 4, -3, 5, 10 ; 6, 2, -7, 0;9 4 Error in HuynhD_Labi (line 9) A = size(x); No fx >> 5 6 7 8 - 9 - 10 11 12 13 % If the matrix is square it will execute tasks 2,3,4, notsamat = 1; A = size(x); if A(1) A(2) notsamat = 1 == 14 % Task 2a 15 16 17 18 19 firstvec = sort(B, 'descend'); firstvec(1,:); revec = secvec = sort(B, 2); resecvec = secvec(:,1); newresecvec = flip(resecvec); dot(revec, newresecvec); 1 20 21 22 23 - 24 25 26 27 - 28 29 % Task 2b %Finding the largest magnitude term in each column for q = 1 : A(2) larmag(q) abs (x(1,9)); for z = 1 : x(1) hn : -bell- lauanlal = % Task 2b %Finding the largest magnitude term in each column for q = 1 : A(2) larmag(q) abs(x(1,9)); for z = 1 : x(1) if abs(x(z,9)) > larmag(q) larmag(q) abs (A(2,9)); end if abs(x(z,9)) larmag(q) C(9,1) = z; C(9,2) end end end == = 9: for f = 1 : A(2) D(f) = abs (A(C(f,1),((f,2))); end E = abs(CCB(2),:)); %Finds the smallest magnitude numbers in each of the matrix's co = % Concatenating into a N x 2 matrix F zeros(B(1), 2); F(:,1) E; F(:,2) = D; C - cortroue (F). % Concatenating into a N x 2 matrix F = zeros(B(1),2); F(:,1) = E; F(:,2) = D; G = sort rows (F); = = 1 % Finding the smallest magnitude numbers for nn = 1 : A(1) smallmag(nn) = abs(x(nn,1)); for mm = 1:A(2) if abs(x(nn, mm)) of 4 - ZOOM Task #1 - Confirm that the matrix is square Check that the matrix is squarc. If it is square, your code should perform Tasks #2, #3, and #4. If the matrix is not square, your code should perform only Task #4. Use a simple if-else statement to control which tasks your code performs. Hint: Check out the size built-in function. Task #2 - MATLAB built-in functions For this task, you may NOT use the built-in function diag Hint: Check out these built-in functions: max, min, abs, transpose ('), flip, dot, and sort rows. a. Please do not use any for loops in this subtask, Calculate the dot product of two vectors. The first vector should contain the most positive (least negative) value in each column of the matrix, in order of column number. The second vector should contain the most negative (least positive) number in each row of the matrix, in reverse order of row number. Lab #1 EMAE 250 Pg. 1 b. Calculate the dot product of two vectors. The first vector should contain the largest magnitude term each column of the matrix, in descending order of the magnitude of the most negative (least positive) term in cach column. The second vector should contain the smallest magnitude term in cach row of the matrix, in descending order of the magnitude of the diagonal term in each row. To create each of these vectors, I recommend a for loop and matrix concatenation to create an Nx2 matrix (N is the size of the input matrix. Then use the sortrows built-in function to re-order the matrices. See the example. Page of 4 ZOOM b. Calculate the dot product of two vectors. The first vector should contain the largest magnitude term in cach column of the matrix, in descending order of the magnitude of the most negative (least positive) term in each column. The second vector should contain the smallest magnitude term in each row of the matrix, in descending order of the magnitude of the diagonal term in each row. To create each of these vectors, I recommend a for loop and matrix concatenation to create an Nx2 matrix (N is the size of the input matrix. Then use the sortrows built-in function to re-order the matrices. See the example. Task #3 - Check to see if matrix is positive definite Later in the semester we'll run across different matrix properties not covered in the primer. One of them is the idea of a positive definite matrix, One way to determine if a matrix is positive definite is to check the determinant of all the co-diagonal submatrices that contain the (1.1) term. If they are all positive, then the matrix is positive definite. Use a while loop to identify and lake the determinant of each of the co-diagonal submatrices of the passed-in matrix. If they are all positive, then the matrix is positive definite, if any of them is zero or negative, then the matrix is not positive definite, Hint: det calculates the determinant of a matrix This is an example of a somewhat common task in programming: determine if ALL members of some set meet one or more criteria. The simplest way to perform this task is as follows: assume all members of the set meet the criteria - this takes the form of setting some variable to 1 (or true) search through the members of the set one at a time-once a member of the set does not meet the criteria, reset the above variable to 0 (or false) and stop searching Task #4 - Compile the output vector If the matrix is not square, your program should return the single value of 0 (zero). If the matrix is square, your program should return a column vector containing the following values: a. The first row of the vector should contain the single value calculated from Task #2.a b. The second row of the vector should contain the single value calculated from Task #2.b. c. The third row of the vector should contain 1 (one) if the matrix is positive definite and 0 (zero) if the matrix is not positive definite