CAN U PLEASE ANSWER QUESTION C PART OF THIS QUESTION EXPLAINING

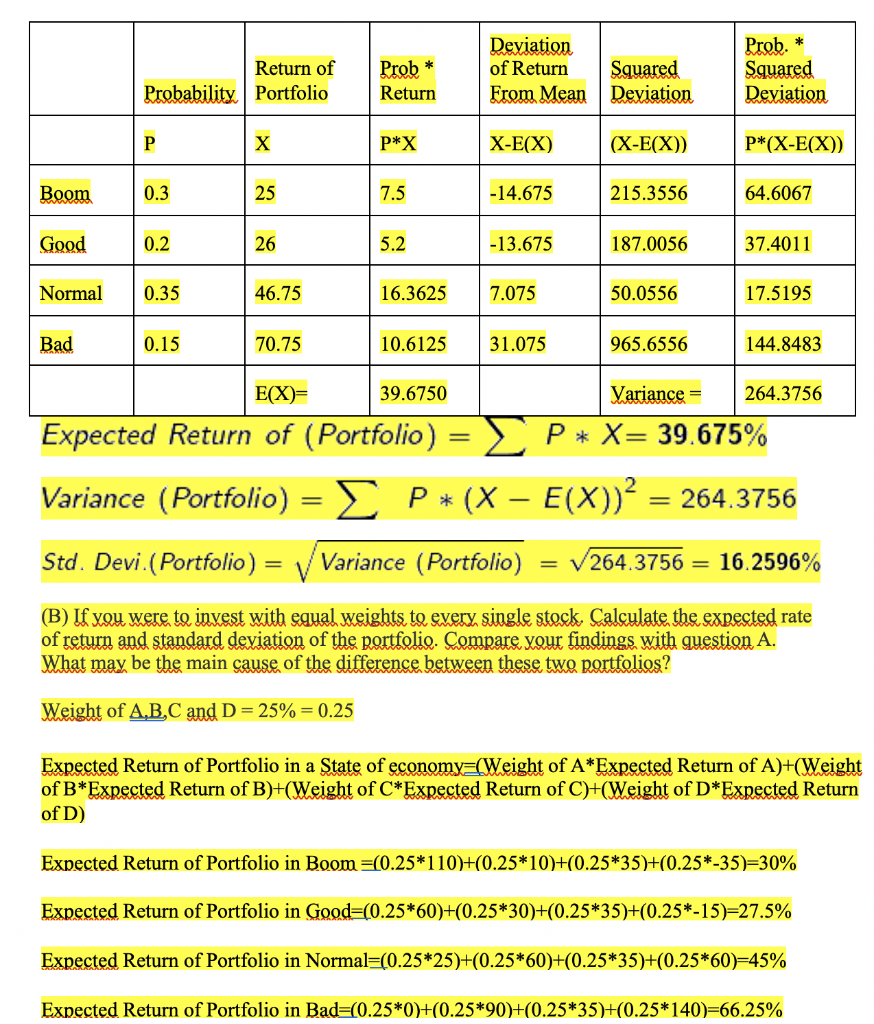
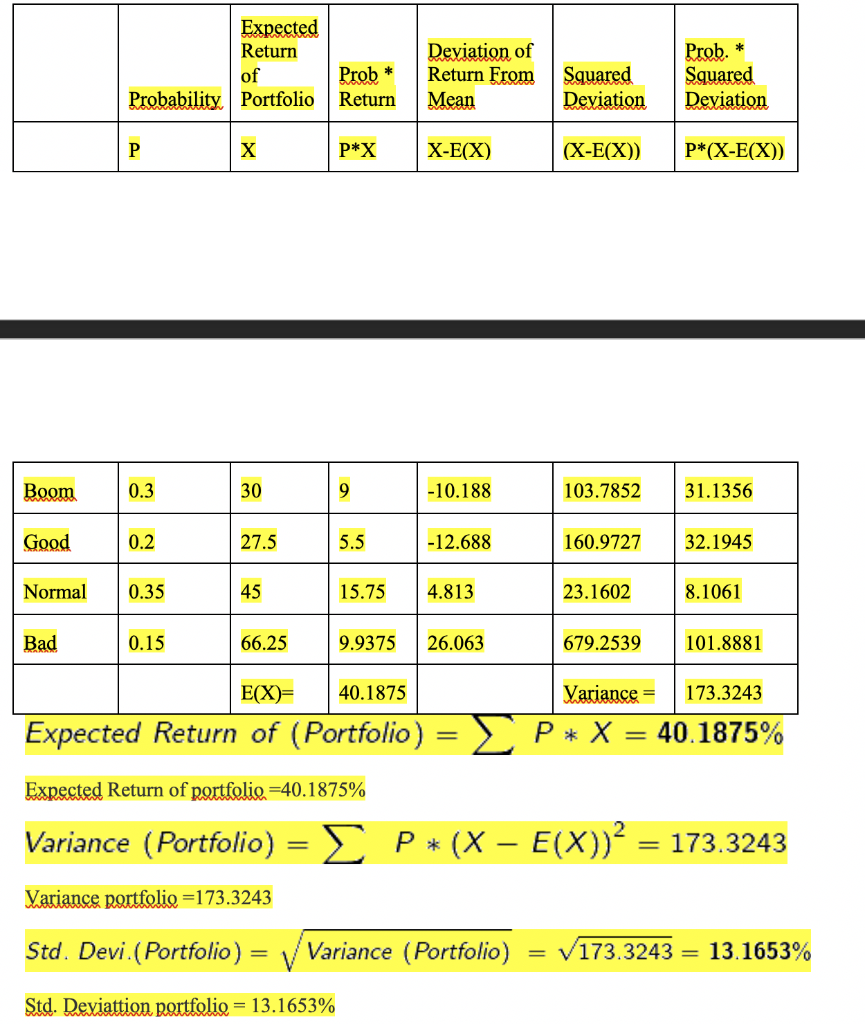
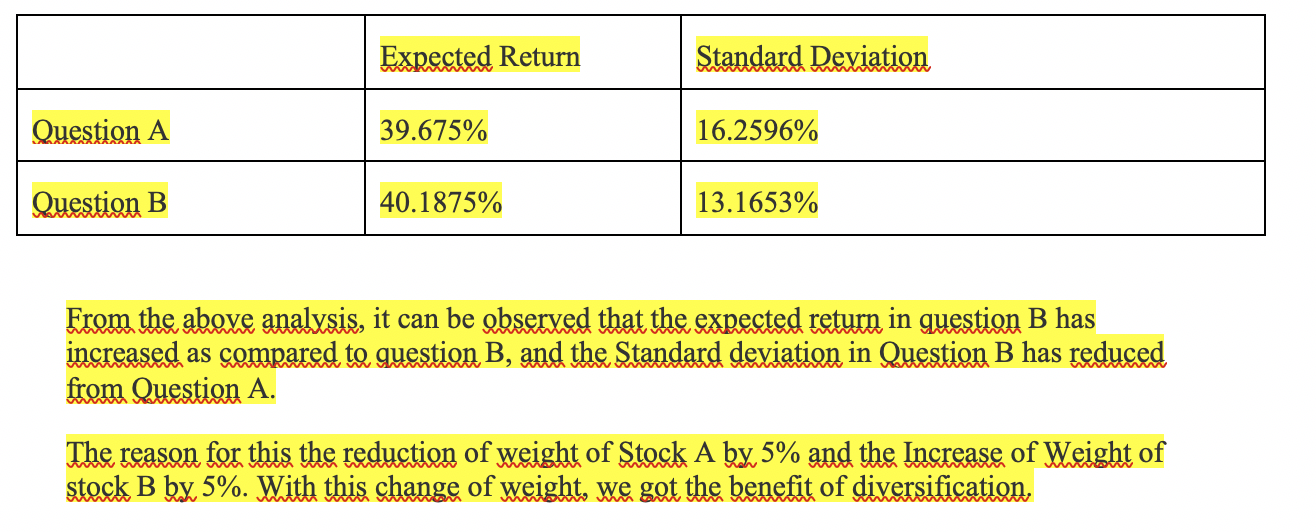
Que 5. Use the stock returns given in the following table under different economic conditions. In you invest %30 of your wealth to Stock A, %20 of your wealth to Stock B, %25 of your wealth to Stock C and %25 of your wealth to Stock D. a) Calculate the expected rate of return and standard deviation of the portfolio. b) If you were to invest with equal weights to every single stock. Calculate the expected rate of return and standard deviation of the portfolio. Compare your findings with question A. What may be the main cause of difference between these two porfolios. c) To obtain a zero standard deviation on a portfolio of your construction with Stock A and D. Calculate the weights that should be assigned to these Stocks. Hint Wa + Wd=1 Econ. Condition Boom Good Normal pr.35 Bad p=30 p=.20 A 110 60 25 0 B 10 30 60 90 35 35 35 35 D -35 -15 60 140 p=.15 (A) Calculate the expected rate of return and standard deviation of the portfolio Weights; A: 30%= 0.30 B: 20%= 0.20 C: 25% = 0.25 D: 25%= 0.25 Return of Portfolio in a State of economy=(Weight of A*Return of A)+(Weight of B*Return of B)+(Weight of C*Return of C)+(Weight of D*Return of D) Return of Portfolio in Boom =(0.2*110)+(0.3*10)+(0.25*35)+(0.25*-35)= 25% Return of Portfolio in Good=(0.2*60)+(0.3*30)+(0.25*35)+(0.25*-15)=26% Return of Portfolio in Normal=(0.2*25)+(0.3*60)+(0.25*35)+(0.25*60)= 46.75% Return of Portfolio in Bad=(0.2*0)+(0.3*90)+(0.25*35)+(0.25*140)= 70.75% Prob. * Prob * Return of Probability Portfolio Deviation of Return Squared From Mean Deviation Squared Deviation Return P X P*X X-E(X) (X-E(X)) P*(X-E(X)) Boom 0.3 25 7.5 -14.675 215.3556 64.6067 Good 0.2 26 5.2 -13.675 187.0056 37.4011 Normal 0.35 46.75 16.3625 7.075 50.0556 17.5195 Bad 0.15 70.75 10.6125 31.075 965.6556 144.8483 E(X)= 39.6750 Variance = 264.3756 Expected Return of (Portfolio) = L P* X= 39.675% Variance (Portfolio) = P*(X E(X))? 264.3756 Std. Devi (Portfolio) = Variance (Portfolio) = V264.3756 = 16.2596% (B) If you were to invest with equal weights to every single stock. Calculate the expected rate of return and standard deviation of the portfolio. Compare your findings with question A. What may be the main cause of the difference between these two portfolios? Weight of A,B,C and D= 25% = 0.25 Expected Return of Portfolio in a State of economy=(Weight of A*Expected Return of A)+(Weight of B*Expected Return of B)+(Weight of C*Expected Return of C)+(Weight of D*Expected Return of D) Expected Return of Portfolio in Boom =(0.25*110)+(0.25*10)+(0.25*35)+(0.25*-35)=30% Expected Return of Portfolio in Good=(0.25*60)+(0.25*30)+(0.25*35)+(0.25*-15)=27.5% Expected Return of Portfolio in Normal=(0.25*25)+(0.25*60)+(0.25*35)+(0.25*60=45% Expected Return of Portfolio in Bad=0.25*0)+(0.25*90)+(0.25*35)+(0.25*140)=66.25% Expected Return of Probability Portfolio * Prob Return Deviation of Return From Mean Squared Deviation Prob. Squared Deviation P P*X X-E(X) (X-E(X)) P*(X-E(X)) Boom 0.3 30 9 -10.188 103.7852 31.1356 Good 0.2 27.5 5.5 -12.688 160.9727 32.1945 Normal 0.35 45 15.75 4.813 23.1602 8.1061 Bad 0.15 66.25 9.9375 26.063 679.2539 101.8881 E(X)= 40.1875 Variance = 173.3243 P* X = 40.1875% Expected Return of (Portfolio) Expected Return of portfolio =40.1875% Variance (Portfolio) = P*(X E(X))2 = = 173.3243 Variance portfolio =173.3243 Std. Devi.(Portfolio) Variance (Portfolio) 173.3243 = 13.1653% Std. Deviattion portfolio = 13.1653% Expected Return Standard Deviation Question A 39.675% 16.2596% Question B 40.1875% 13.1653% From the above analysis, it can be observed that the expected return in question B has increased as compared to question B, and the Standard deviation in Question B has reduced from Question A. The reason for this the reduction of weight of Stock A by 5% and the Increase of Weight of stock B by 5%. With this change of weight, we got the benefit of diversification