Question: can you explain how to do it with proof Let V be an inner product space with inner product (., .), and let SE C(V)

can you explain how to do it with proof

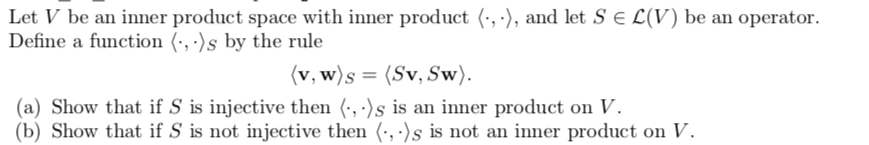
Let V be an inner product space with inner product (., .), and let SE C(V) be an operator. Define a function (., .)s by the rule (v, w)s = (Sv, Sw). (a) Show that if S is injective then (, .)s is an inner product on V. (b) Show that if S is not injective then (., .)s is not an inner product on V

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Abstract Linear Algebra - Math 416 Spring 2015 Homework 11 1. Let V be an inner product space, and let x, y V . Show that if x y, then x+y 2 = x 2 + y 2 . 2. For each of the following inner products,...

Label the following statements as true or false. You do NOT need to justify your answers. I [ ] Let V be a inner product space with ordered basis B. Let T be a linear operator on V, then the ajoint...

the 2 questions are separate(no relationship) 1) Let V be an inner product space and let W be a k-dimensional subspace of V. Furthermore, let B = {v1, U2, ..., Uk} be an orthonormal basis of W. We...

Question 6: Let V be an inner product space. For a xed vector v0 in v, dene T: v ' R by T(v) 2 (v, v0}. Prove that T is a linear transformation Let \"'0 be a vector in inner product space V, and dene...

1. Let V be an inner product space. A linear transformation T : V ) V is called an isometry if ||T(v)|| = "s" for all 1: 6 vi] (a) Show that the following linear transformation is an isornetrgg.r on...

!!!!!!!!!!!!! Let (V, (, )) be an inner product space. For all w, v E V and scalar A, we have that | |vl| = | |w|| implies that ||ull = ||(-A)wll. Select one: True O False Let (V, (, )) be a complex...

thank you Let V be an inner product space with inner product ( , ), and let 5 be an element of V. Show that the mapping L3 : V > IR defined by L3(x) = (x, v) is a linear mapping

I want to know the step-by-step answer to this question. Thanks! Question 3 [4pts] Let V be an inner product space with inner product ( , ), and let 1? be an element of V. Show that the mapping L5 :...

Let V be the inner product space consisting of R^2 and the inner product whose quadratic form is defined by ||(x_1, x_2)||^2 = (x_1, x_2)^2 + 3(x_2)^2. Let E be the orthogonal projection of V onto...

How can I solve this question 4? (linear algebra) Question 4a [4pts] Let V be an inner product space with inner product ( , ), and let X1, . ..In, ye V. Use proof by induction to show that n n y =...

Currently shares of ABC Company is trading for $74 per share in the market. The company recently paid $4.5 dividend per share and expected to pay $4.725 dividend next year. The company follows a...

component reliability for the redesigned product? 16. A Quality Manager at an Auto Body Shop visually inspects 25 re-sprayed vehicles each week for "aesthetics. The Quality Manager will reject any...

Segmented income statements are prepared using the blank format. (Enter only one word per blank.)

2023 1040 form 1.Phillip and Claire are married and file a joint return. Phillip is self-employed as a real estate agent, and Claire is a flight attendant. Phillip and Claire have three dependent...