Can you help me solve the problem 4?

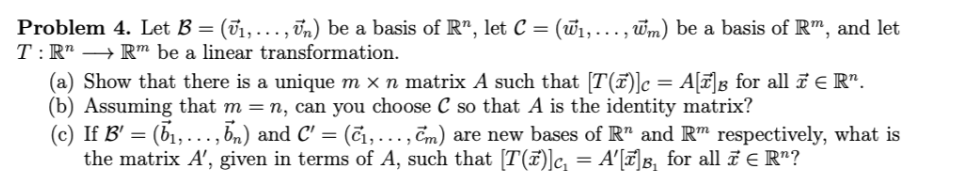
Problem 4. Let B = (U1, . .., Un) be a basis of R", let C = (w1, ..., Wm) be a basis of Rm, and let T : R" -> Rm be a linear transformation. (a) Show that there is a unique m x n matrix A such that [T(T)]c = As for all i E Rn. (b) Assuming that m = n, can you choose C so that A is the identity matrix? (c) If B' = (b1, . .., bn) and C' = (C1, . .., Cm) are new bases of R" and Rm respectively, what is the matrix A', given in terms of A, such that [T(D)]c, = A'[x]B, for all i E R"